A casa nostra abbiamo tutti il proprio letto, solo papà deve dormire dalla mamma

ELETTRONICA

… studiare, studiare ed ancora studiare, è il solo modo di capire quanto possa essere grande sia la propria ignoranza!

Massa

kilogrammo

FORZE TRA CONDUTTORI PARALLELI-INDUZIONE ELETTROMAGNETICA

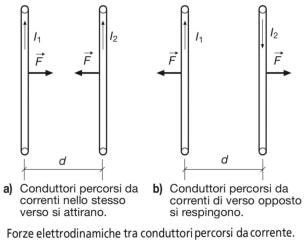
Forze agenti tra conduttori paralleli Tra due conduttori percorsi da corrente, considerati per semplicità rettilinei e paralleli, si instaurano delle forze, di attrazione o di repulsione a seconda dei versi delle correnti, dovute al campo magnetico creato da un conduttore e agente sull’altro. La forza agente su ogni conduttore è direttamente proporzionale al prodotto delle correnti e inversamente proporzionale alla distanza tra i conduttori : figure a) e b). Questo fenomeno fu evidenziato per la prima volta mediante l’esperienza di Ampère e le forze agenti sui conduttori sono comunemente dette forze elettrodinamiche

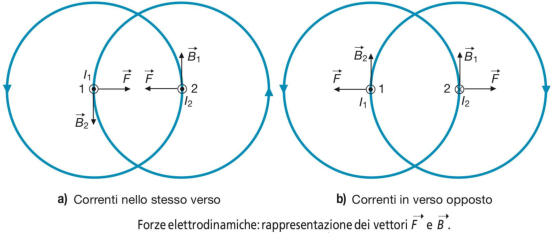
Nelle sottostanti figure c) e d) è stata rappresentata la situazione che si crea su un piano perpendicolare al conduttore, nei due casi di correnti concordi (c) e discordi (d).

Supponendo di essere nel vuoto (o nell’aria, avente quasi la stessa permeabilità magnetica), l’intensità del vettore induzione creato dalla corrente I1 nel punto in cui è posto il condut- -tore 2 è data dalla relazione:

Sul conduttore 2 agirà la forza F, che dipende dalla corrente I2 e dall’induzione B1: F = B1I2l, essendo l la lunghezza comune dei due conduttori. Sostituendo si ha:

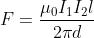
Facendo lo stesso ragionamento per il conduttore 1, soggetto all’induzione B2, si ottiene la stessa espressione. Nel caso di conduttori posti in un mezzo magnetico di permeabilità μr≠ 1, occorre considerare la permeabilità del mezzo invece di quella del vuoto, ottenendo:

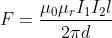
e la forza diventa maggiore, dipendentemente dal valore di μr. Nel caso di due conduttori percorsi dalla stessa corrente (come i due fili di andata e ritorno di un cavo elettrico), si ha I1= I2= I e, quindi:

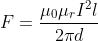
Quanto è stato detto a proposito delle forze elettrodinamiche si può così riassumere: due conduttori paralleli, percorsi da corrente, sono soggetti ognuno a una forza di attrazione (correnti concordi) o di repulsione (correnti discordi), che aumenta con il prodotto delle intensità delle due correnti (o con il loro quadrato, se uguali), con la permeabilità del mezzo magnetico dove sono posti i conduttori e con la lunghezza degli stessi; la forza diminuisce, invece, all’aumentare della distanza tra i conduttori.

Esempio: Calcolare le forze elettrodinamiche agenti per ogni metro di lunghezza su due conduttori, percorsi dalla stessa corrente I = 100 A, posti a distanza di 5 cm, nei seguenti due casi: in aria e all’interno di una materiale ferromagnetico con μr = 2000. Usando l’espressione considerata, con l = 1 m, μr = 1 e μr = 2000 per i due casi, si ha:

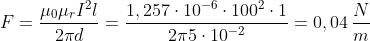
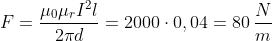
Induzione elettromagnetica Il fenomeno dell’induzione elettromagnetica (da non confondere con il vettore induzione magnetica), scoperto nella prima metà dell’800, consiste nella generazione di tensioni e di correnti indotte all’interno di circuiti elettrici, interessati da un campo magnetico variabile. La variabilità del campo magnetico, e più precisamente del flusso magnetico concatenato con il circuito, è proprio la condizione imprescindibile affinché vi sia nel circuito la nascita di una tensione indotta, cioè provocata dalla variazione del flusso, e di una conseguente corrente, se il circuito è chiuso.

Se il circuito si concatena con un flusso costante nel tempo, non si crea alcuna tensione e non circola in esso alcuna corrente. Vari esperimenti hanno verificato tale fenomeno e hanno mostrato che il valore della tensione indotta è direttamente proporzionale alla variazione ΔΦc del flusso concatenato e inversamente proporzionale all’intervallo di tempo Δt durante il quale si ha tale variazione, secondo la relazione:

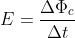
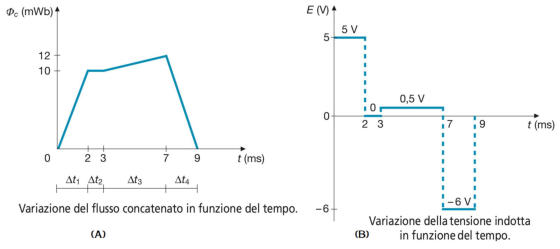
nota come legge di Faraday-Neumann. L’espressione indica che la tensione indotta è pari al rapporto incrementale tra le grandez- -ze Φc e t e quindi dipende dalla pendenza della curva che lega le due grandezze: quanto maggiore è la pendenza tanto più grande è la variazione ΔΦc a parità di Δt e quindi tanto più elevata è la tensione indotta.

Quest’ultima equazione giustifica anche la relazione che lega il weber al volt: essendo ΔΦc = E Δt, si ha che 1 Wb = 1 V × 1 s.

Esempio: Calcolare la tensione indotta in un circuito che si concatena con un flusso variabile nel tempo secondo il grafico riportato in figura.

L’intervallo di tempo considerato può essere diviso in quattro intervalli elementari, durante i quali il flusso varia linearmente, la pendenza dei singoli tratti rimane costante e, di conseguenza, è costante anche la tensione indotta. I valori degli intervalli di tempo e delle rispettive variazioni di flusso concatenato sono pari a:

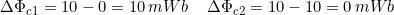
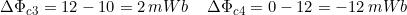
Applicando la relazione conosciuta, si ricavano i corrispondenti valori della tensione indotta:

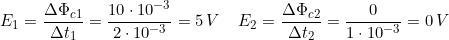
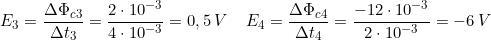
il cui grafico, in funzione del tempo, è riportato nella figura (B), dalla quale si può notare che: • negli intervalli di tempo in cui la pendenza è maggiore si ha la maggiore tensione indotta; • negli intervalli di tempo in cui il flusso concatenato rimane costante la tensione indotta è nulla; • negli intervalli di tempo in cui il flusso concatenato diminuisce (variazione negativa) si inverte il segno della tensione.

Se il circuito che subisce il fenomeno dell’induzione elettromagnetica è chiuso e non vi è alcun altro generatore in grado di far circolare corrente, la tensione indotta si comporta da forza elettromotrice e genera una corrente che, a sua volta, provoca un campo magnetico indotto. Esperimenti successivi a quelli di Faraday hanno dimostrato che la corrente indotta genera un campo magnetico che si oppone alle variazioni di quello induttore; se il flusso conca- -tenato induttore tende a diminuire il campo indotto ha un effetto magnetizzante, concorde con quello induttore, e viceversa. Queste osservazioni hanno portato alla formulazione della legge di Lenz: il verso della tensione indotta è sempre tale da opporsi alla variazione del flusso concatenato induttore. Per tener conto di tale opposizione, nella precedente relazione, viene spesso posto il segno “–”, esprimendo matematicamente la legge di Faraday-Neumann-Lenz nel modo seguente:

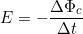
Nel prosieguo della trattazione si userà spesso anche la formulazione senza il segno: il non tenere conto del segno “−” è una procedura corretta se, nell’attribuire il verso della tensione indotta, si tiene conto del fatto che la stessa deve opporsi alla variazione del flusso induttore. Dall’espressione della Legge di Faraday-Neumann, si ricava:

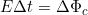
Il prodotto EΔt, pari alla variazione del flusso concatenato, è detto anche impulso di tensione; esso si misura in weber o in volt per secondo e corrisponde, sul grafico E = f(t), all’area del rettangolo elementare avente altezza E e base Δt

Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara