Non legare il cuore a nessuna dimora, perché soffrirai quando te la strapperanno via.

ELETTRONICA

… studiare, studiare ed ancora studiare, è il solo modo di capire quanto possa essere grande sia la propria ignoranza!

Massa

kilogrammo

INTERAZIONE TRA CIRCUITI ELETTRICI E CAMPI MAGNETICI

In questo capitolo verranno presentati alcuni fenomeni dell’elettromagnetismo che rivestono particolare interesse per le loro applicazioni in campo elettrico, in quanto costitu- -iscono i principi fondamentali su cui si basa il funzionamento di varie apparecchiature, dalle macchine elettriche (trasfo- -rmatore, motori e generatori elettrici) agli strumenti di misura analogici (amperometri, voltmetri, wattmetri ecc.).

Forza agente su un conduttore elettrico Nelle pagine precedenti è stata introdotta l’esperienza di Faraday, secondo la quale su un filo conduttore, percorso da corrente elettrica e posto in un campo magnetico, si sviluppa una forza che, considerata come grandezza vettoriale, ha le seguenti caratteristiche:

• intensità F = BIl direttamente proporzionale al valore dell’induzione magnetica nel punto in cui è posto il conduttore, all’intensità della corrente e alla lunghezza della parte di conduttore interessata dal campo magnetico; • direzione perpendicolare sia al campo magnetico che alla corrente; • verso individuato dal pollice della mano sinistra disposta lungo il conduttore nel senso della corrente, con le linee di forza del campo entranti nel palmo della mano.

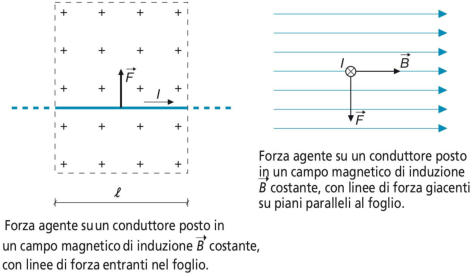
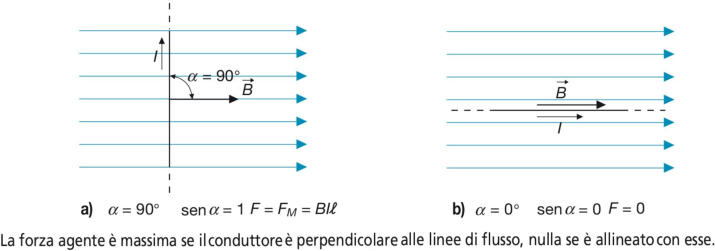
Le soprastanti figure mostrano la direzione e il verso del vettore , secondo due diverse rappresentazioni grafiche: nella prima figura le linee di forza del campo magnetico sono perpendicolari al piano del disegno ed entranti nello stesso (indicate dai segni +++ ...), nella seconda la corrente è perpendicolare al piano del disegno ed entrante nello stesso (indicata dalla coda della freccia), mentre le linee di campo giacciono sul piano del disegno e su quelli a esso paralleli, per una certa lunghezza l. In ogni caso la lunghezza da considerare è sempre quella interessata dalle linee del campo magnetico; la parte di conduttore fuori dall’azione del campo magnetico non è soggetta ad alcuna forza. La legge F = BIl vale quando l’induzione magnetica è costante in ogni punto del conduttore elettrico. In caso contrario bisogna dividere il conduttore in tanti tratti elementari, di lunghezza , su ognuno dei quali l’induzione magnetica, supposta perpendicolare al tratto di conduttore, vale , calcolare le forze elementari su ognuno dei tratti con la legge e sommare vettorialmente le varie forze, calcolandone la risultante.

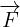
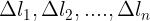
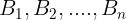
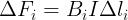
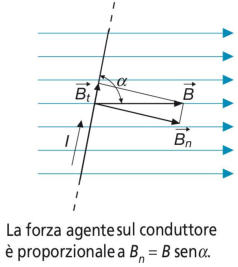
Si consideri ora la figura a sinistra, un conduttore disposto non perpendicolarmente alla direzione delle linee di forza di un campo magnetico costante, avente la stessa induzione magnetica B in ogni punto. Il vettore può essere scomposto in due vettori componenti, perpendicolare al conduttore e nella direzione del conduttore stesso. La forza esercitata dal campo magnetico è dovuta alla componente normale dell’induzione, pari a Bn= B senα e quindi si avrà:

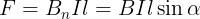
A seconda del valore di α la forza varierà, assumendo il valore massimo FM= BIl quando α = 90° (figura A) e il valore zero quando α = 0° (figura B). Quindi un conduttore immerso in un campo magnetico avente la stessa direzione della corrente non è soggetto ad alcuna forza.

Esempio: Un conduttore di lunghezza l = 0,5 m, percorso dalla corrente I = 10 A, è posto in un campo magnetico di induzione costante B = 1 T. Calcolare la forza agente sul conduttore nei seguenti casi: α = 30°, α = 45°, α = 60°, α = 90°.

Applicando la formula per i quattro casi previsti si ha:

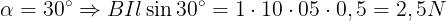
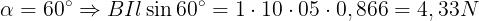
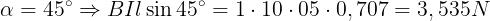
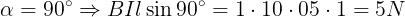
Coppia agente su una spira

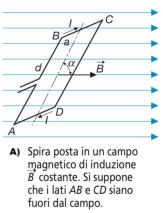
Si consideri come in figura (A) una spira elettrica, percorsa dalla corrente I, posta in un campo magnetico di induzione costante, con linee di forza parallele tra loro. I lati BC e AD (lati attivi) sono posti all’interno del campo per una lunghezza a, mentre i lati AB e CD, di lunghezza d, sono fuori dal campo magnetico. Su ognuno dei lati attivi agirà una forza perpendicolare a e al conduttore, come mostrato nella rappresentazione piana di figura (B).

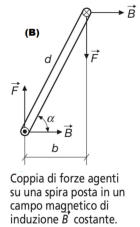
La forza agente su ogni conduttore di lunghezza a è data da: F = BIa. Essendoci due forze uguali, parallele e di verso opposto, sulla spira agirà una coppia di forze, il cui momento è dato da: C = Fb = BIab, dove b è il braccio della coppia, legato alla dimensione d della spira e all’angolo α di inclinazione della spira rispetto alle linee di campo, secondo la relazione b = d cosα di figura ( C). Sostituendo nell’espressione del momento si ha:

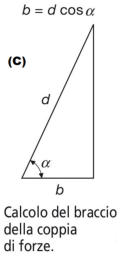
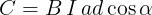
Il prodotto ad tra le dimensioni della spira è pari all’area S della sua sezione interna e, quindi, si ottiene:

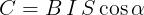
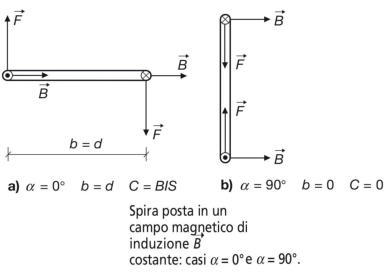
L’espressione enunciata mostra che il momento della coppia (o, semplicemente, la coppia) agente sulla spira varia in funzione dell’angolo α, con valori estremi dati da: • C = CM = BIS quando α = 0° (cosα = 1), ossia quando il piano della spira è parallelo alle linee di campo e il braccio della coppia è massimo (figura a); • C = 0 quando α = 90° (cosα = 0), ossia quando il piano della spira è perpendicolare alle linee di campo e il braccio della coppia è nullo (figura b).

Coppia prodotta da un campo magnetico radiale Per avere una coppia costante, indipendente dalla posizione della spira, il campo magnetico deve essere radiale, ossia con le linee di forza dirette tutte verso il centro della spira e perpendicolari in ogni punto alla circonferenza che la spira stessa descriverebbe con un movimento rotatorio intorno al proprio centro. In questo caso il braccio delle forze è sempre pari alla dimensione d e, quindi, si ha

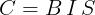
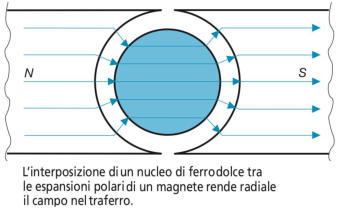
per qualsiasi posizione della spira. Un modo per ottenere un campo magnetico radiale è quello di porre, tra le espansioni polari di un magnete, un nucleo cilindrico di ferro dolce, in grado di modificare l’andamento delle linee di forza e di renderle radiali nel traferro circostante il nucleo stesso, evidenziato nella figura sottostante.

Coppia agente su una bobina Se invece di una spira si considera una bobina di N spire, ogni lato sarà composto da N conduttori e quindi la forza agente su un lato sarà pari a N volte quella relativa a una spira, come pure la coppia totale ottenuta. Si avrà pertanto:

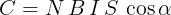
oppure:

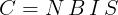
a seconda che la coppia sia dovuta a un campo con linee di forza parallele o radiali

Esempio: Calcolare la coppia agente su una spira quadrata, di dimensioni 10 × 10 cm, percorsa dalla corrente I = 5 A e posta in un campo magnetico di induzione costante B = 1 T con linee di forza parallele, nelle seguenti posizioni: α = 0°, α = 30°, α = 60°, α = 90°

La sezione della spira è S = 10 × 10 = 100 cm2 = 100 × 10 – 4 m2; applicando la nota formula per i diversi valori dell’angolo si ottiene:

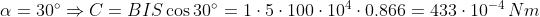
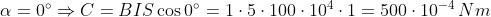
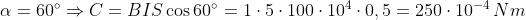
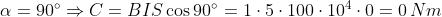
Esempio: Ripetere l’esempio precedente nel caso di una bobina di 100 spire posta in un campo magnetico con linee di forza radiali

In questo caso occorre applicare la nota espressione, dato che il valore di C è indipendente dalla posizione:

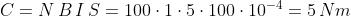
e il valore che si ottiene è pari a 100 volte quello del precedente esempio, nel caso α = 0°

Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara