Tutti i bambini sono degli artisti nati; il difficile sta nel fatto di restarlo da grandi

ELETTRONICA

… studiare, studiare ed ancora studiare, è il solo modo di capire quanto possa essere grande sia la propria ignoranza!

Massa

kilogrammo

ENERGIA DEL CAMPO MAGNETICO

Energia del campo magnetico Quando un circuito elettrico crea un campo magnetico vi è uno scambio di energia: il circuito, durante la fase di magnetizzazione, fornisce energia elettrica all’induttore, energia che, a magnetizzazione conclusa, resta immagaz- -zinata nello spazio interessato dal campo magnetico a livello di energia potenziale, in grado di compiere lavoro, come avviene, per esempio, in un elettromagnete che attira un pezzo di ferro. Durante la smagnetizzazione, invece, l’energia viene restituita al circuito induttore. Per valutare analiticamente il valore dell’energia del campo magnetico si consideri un induttore lineare, di induttanza L costante, con le N spire percorse da una corrente variabile i.

Facendo aumentare i da zero al valore finale I, il flusso concatenato varierà anch’esso da zero a Φc = LI, con la legge lineare = Li, rappresentata dal segmento di retta della sottostante figura:

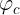
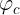
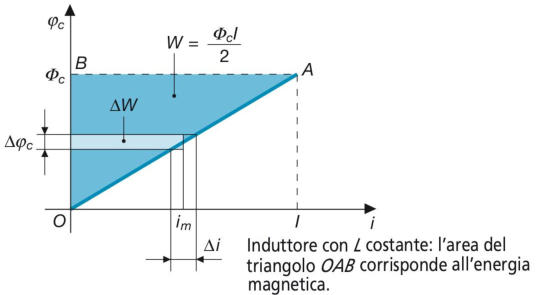
Prendendo in esame l’incremento finito di flusso concatenato Δϕc e considerando il valore medio im della corrente in tale intervallo, l’area del rettangolo evidenziato rappresenta il prodotto . Esso equivale all’incremento di energia elettromagnetica che si ha nell’induttore, conseguente all’incremento del flusso concatenato. Che tale prodotto sia un’energia lo si può vedere esaminando le unità di misura:

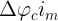
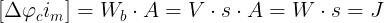
si avrà, quindi :

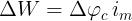
Per calcolare l’energia totale che, in seguito alla magnetizzazione del volume interno all’induttore, resta immagazzinata nel componente, occorre sommare tutti i contributi che si hanno quando il flusso concatenato passa da zero al valore Φc . La somma delle aree dei vari rettangoli corrisponde a quella del triangolo OAB e, quindi:

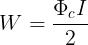
Sostituendo l’espressione si ricava facilmente:

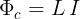
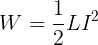
L’energia immagazzinata in un induttore dipende, quindi, dalla sua induttanza e dal valore della corrente magnetizzante, che gioca un ruolo importante in quanto compare al quadrato: un aumento del doppio della I fa aumentare di quattro volte l’energia e così via.

Si noti l’analogia tra l’ultima relazione e la formula dell’energia del campo elettrico: la struttura matematica è la stessa. L e C hanno lo stesso ruolo, mentre vi è lo scambio tra V e I, dato che un condensatore si “carica in tensione”, a differenza dell’induttore, per il quale la grandezza che indica il livello di magnetizzazione è la corrente. Operando sulle relazioni già enunciate con le leggi che legano le grandezze magnetiche, si ottengono altre utili espressioni dell’energia del campo magnetico:

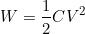
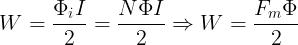
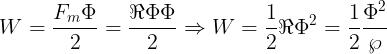
Esempio : Calcolare l’energia magnetica immagazzinata in un induttore di induttanza L = 5 mH, quando la corrente vale 2 A. Calcolarne inoltre la riluttanza, sapendo che la bobina è composta da 100 spire.

Si calcola l’energia magnetica:

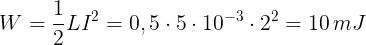
l flusso magnetico è dato da:

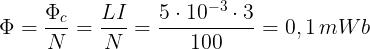
La riluttanza del circuito magnetico si calcola con la formula inversa:

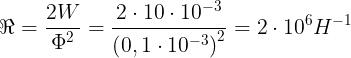
Energia magnetica specifica Per energia magnetica specifica si intende il rapporto tra l’energia del campo magnetico e il volume del mezzo magnetico sede del campo stesso e quindi essa rappresenta l’energia magnetica per unità di volume, espressa in joule su metro cubo. Nel caso di un induttore di lunghezza l e sezione S, il volume è dato da lS e l’energia dalla relazione già vista: Tenendo conto che Fm= Hl e Φ = BS, si avrà:

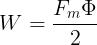
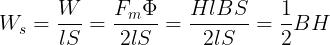
Usando la relazione B = μH si ottengono le espressioni equivalenti:

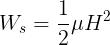
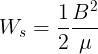
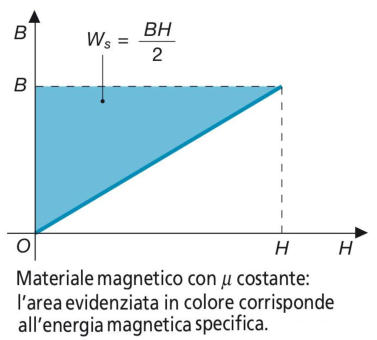
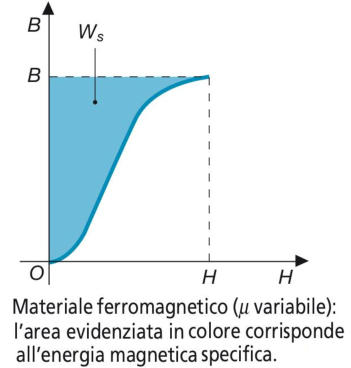
Nel caso di materiale magnetico con permeabilità costante, la legge B = μH è l’equazione di una retta passante per l’origine e la formula Ws=BH/2 corrisponde all’area del triangolo evidenziato sulla caratteristica di magnetizzazione di figura:

La corrispondenza tra l’area compresa fra la curva di magnetizzazione e l’asse delle ordinate e l’energia magnetica specifica vale, in realtà, anche se la caratteristica non è lineare, come in figura:

Esempio: Calcolare l’energia magnetica specifica del solenoide rettilineo composto da 200 spire avvolte su un nucleo non ferromagnetico, di diametro 2 cm e lunghezza 10 cm, quando la corrente magnetizzante è pari a 5 A.

La forza magnetizzante è data da:

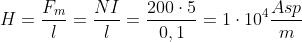
L’energia specifica si calcola :

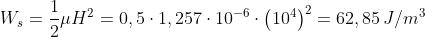
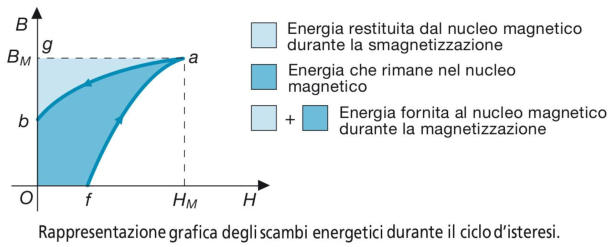
Si consideri il sottostante diagramma, una parte del ciclo d’isteresi di un materiale ferromagnetico, composto dalla curva di magnetizzazione f-a e da quella di smagnetizzazione a-b. Durante le varie fasi del ciclo vi è uno scambio di energia tra il circuito esterno e l’induttore sede del campo magnetico, precisamente: • durante la magnetizzazione il circuito esterno fornisce energia, che viene immagazzinata nello spazio sede del campo magnetico; • durante la smagnetizzazione l’induttore restituisce energia al circuito

Energia persa durante il ciclo di isteresi

Nel caso in esame l’energia specifica fornita durante la magnetizzazione corrisponde all’area della figura piana O-f-a-g, mentre quella restituita durante la smagnetizzazione è data dall’area della figura b-a-g. Dato che le due curve non coincidono, l’energia restituita è minore di quella fornita e la differenza corrisponde all’area della figura interna O-f-a-b. Considerando tutto il ciclo d’isteresi succede che per ogni ciclo la differenza tra l’energia specifica fornita dal circuito elettrico magnetizzante e quella restituita a tale circuito corrisponde all’area interna del ciclo d’isteresi ed è, quindi, tanto più elevata quanto maggiore è l’area del ciclo stesso. Questa energia si trasforma in calore, producendo il riscaldamento del nucleo magnetico. Il valore dell’energia persa nell’unità di tempo corrisponde a una potenza, detta perdita per isteresi magnetica.

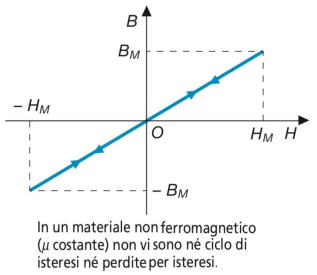
Nei materiali non ferromagnetici, di permeabilità costante, il fenomeno non si verifica, in quanto, essendo le caratteristiche di magnetizzazione e smagnetizzazione lineari e coincidenti, non vi è isteresi e l’area interna alle curve è nulla, come nel soprastante diagramma.

Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara