I bambini vengono educati da quello che gli adulti sono e non dai loro discorsi.

ELETTRONICA

… studiare, studiare ed ancora studiare, è il solo modo di capire quanto possa essere grande sia la propria ignoranza!

Massa

kilogrammo

LEGGE DELLA CIRCUITAZIONE MAGNETICA - L’INDUTTANZA

Legge della circuitazione magnetica Si consideri la relazione che consente di calcolare la forza magnetizzante, sia per un solenoide rettilineo che toroidale, dando l’opportuno valore a l. Da essa si ricava facilmente l’espressione: che sancisce l’uguaglianza tra la f.m.m. e il prodotto Hl.

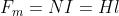
A quest’ultima espressione si può dare un’interpretazione più generale: considerata una linea di forza chiusa, scomponibile in tratti elementari di lunghezza , per ognuno dei quali il vettore H agisce nella direzione della linea di forza, con intensità , vale la relazione:

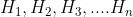
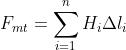
dove il primo termine è la f.m.m. totale agente lungo la linea chiusa, somma delle f.m.m. di tutte le bobine magnetizzanti concatenate con la linea considerata, mentre il secondo termine, pari alla somma dei prodotti tra il valore assunto dalla forza magnetizzante e la lunghezza del tratto in cui tale valore si mantiene costante, è detta circuitazione del vettore . La legge precedente prende il nome di legge della circuitazione magnetica e consente di calcolare la f.m.m. necessaria per ottenere un determinato valore della forza magnetiz- -zante nei vari tratti di un circuito magnetico. È importante osservare che la f.m.m. totale va calcolata tenendo conto del segno dei vari contributi, nel senso che se una bobina esercita un’azione magnetizzante opposta a quella assunta come positiva, la sua f.m.m. va considerata negativa nel computo della f.m.m. totale

Esempio : Nel nucleo magnetico in figura, di spessore costante e permeabilità relativa uguale a 1500, la lunghezza della linea di flusso media è pari a lm = 20 cm e la lunghezza della parte in aria (traferro) è δ = 1 mm. Se N1=100 spire e N2=20 spire, calcolare il valore della corrente I per avere una induzione al traferro di 0,5 T

Le due bobine sono collegate in serie, in quanto interessate dalla stessa corrente I. Tenendo conto del senso di avvolgimento e del verso di percorrenza della corrente, si vede che la loro azione magnetizzante è concorde ed è tale da orientare le linee di campo in senso orario. Per verificarlo basta porre il palmo della mano destra nel senso di percorrenza della corrente: il pollice indicherà il verso delle linee di forza. Le due f.m.m. si sommeranno e si avrà:

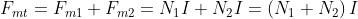
e, quindi, è come se agisse una sola bobina di (N1+ N2) spire.

L’intero percorso della linea di forza può essere diviso in due parti: • una parte, di lunghezza , che si svolge nel materiale ferromagnetico; • una parte, di lunghezza ,che si svolge in aria. I due tratti sono magneticamente in serie, ossia sono interes- -sati dallo stesso valore del flusso magnetico; tutte le linee di forza, infatti, interessano sia il tratto in aria che quello nel materiale ferromagnetico. Le induzioni nei due tratti saranno pari a . 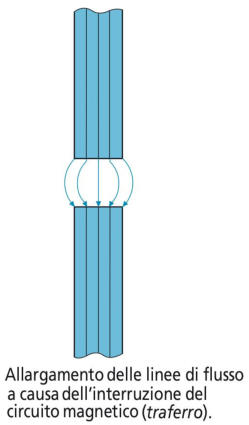Le aree delle due sezioni trasversali alle linee di flusso sono praticamente uguali, in quanto il nucleo ha spessore costante ed è del tutto trascu- -rabile il fenomeno magnetico per il quale, passando dalla parte in ferro a quella in aria, la larghezza del tubo di flusso tende ad aumentare, come in figura. Si può ritenere pertanto che sia:

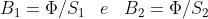
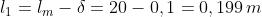
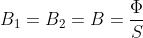
Quello che invece non è costante nei due tratti è il valore della forza magnetizzante, data dal rapporto B/μ, poiché il materiale ferromagnetico e l’aria hanno valori della permeabilità molto diversi tra loro. Tenendo conto del valore dato B = 0,5 T, per i due tratti si avranno i seguenti valori di H :

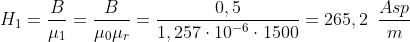
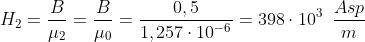
Il valore 1500 volte più elevato di H2 rispetto ad H1 testimonia la maggiore difficoltà che si incontra nel magnetizzare l’aria rispetto a un materiale ferromagnetico. Applicando la legge della circuitazione magnetica alla linea di forza media, concatenata con entrambe le bobine. si ha:

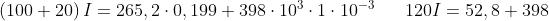
e quindi:

È da notare che la f.m.m. necessaria per magnetizzare il traferro (398 Asp) è, in realtà, non molto maggiore di quella necessaria per la parte in ferro (52,8 Asp), nonostante l’elevata differenza tra i valori di H; questo è dovuto al fatto che la lunghezza del traferro è molto minore di quella del nucleo ferromagnetico.

Esempio: Ripetere il soprastante esempio, nel caso che la bobina di N2 spire venga avvolta in senso opposto all’altra.

In questo caso le due f.m.m. sono discordi e, quindi, si ha:

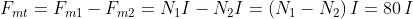
Tutto il resto dell’esercizio rimane uguale; dall’applicazione della legge della circuitazione si ricava:

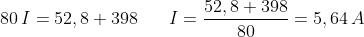
La corrente necessaria per la magnetizzazione è, in questo caso, ovviamente maggiore, dato che una delle due bobine esercita un’azione smagnetizzante.

Induttanza Una bobina elettrica di N spire, avvolta su un nucleo magnetico, che può essere anche di tipo non ferromagnetico come l’aria, costituisce un induttore. L’induttore può essere visto come un bipolo, dato che interagisce con il resto del circuito a cui è collegato mediante due morsetti, come in figura: Come il resistore è caratterizzato dalla resistenza e il condensatore dalla capacità, anche l’induttore ha un parametro che lo identifica, l’induttanza.

Per definire tale parametro si consideri il funzionamento dell’induttore: quando è percorso da una corrente di intensità costante I, esso produce un campo magnetico, le cui linee di forza si concatenano con le spire della bobina, come nel caso del solenoide rettilineo, che è un tipico esempio di induttore. Il prodotto:

tra il flusso magnetico e il numero di spire della bobina è detto flusso concatenato.

Per definizione si considera come induttanza il rapporto:

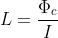
tra il flusso concatenato e l’intensità della corrente che lo ha prodotto.

Se nella precedente relazione, si pone I = 1 A, si vede che numericamente L e Φc coincidono e,quindi, si può dire che l’induttanza rappresenta il valore del flusso concatenato per unità di corrente magnetizzante. L’equazione caratteristica dell’induttore è data da:

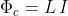
Flusso concatenato in funzione della corrente

Nel caso che sia L costante, la soprastante è l’equazione tipica di una retta passante per l’origine, del tipo y = mx, rappresentata nella figura:

Applicando la legge di Hopkinson, si ottiene:

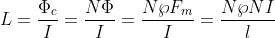
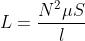
Sostituendo con l’espressione della permeanza, si ha anche

formula che lega l’induttanza di una bobina alle sue caratteristiche costruttive. La sopraenunciata formula, mostra che l’induttanza aumenta con il numero di spire e con la sezione del nucleo su cui è avvolta la bobina, mentre diminuisce all’aumentare della lunghezza del nucleo. Il valore di L dipende anche, in modo direttamente proporzionale, da quello della permeabilità magnetica. È da rilevare inoltre che, per avere un’induttanza costante per tutti i valori della corrente magnetizzante, la permeabilità deve essere costante al variare del grado di magnetizzazione del nucleo. Ciò porta alla seguente conclusione: un induttore si comporta da bipolo lineare, presentando un’induttanza costante, solo quando è costante il valore della permeabilità del nucleo e, quindi, se il materiale usato non è di tipo ferromagnetico o se funziona solo sul tratto lineare della caratteristica di magnetizzazione. L’unità di misura dell’induttanza è l’henry (H); dalla relazione, si vede infatti che L, essendo legato a da un fattore adimensionato, deve avere la sua stessa unità di misura che è, appunto, l’henry.

Esempio: Calcolare l’induttanza di un solenoide rettilineo composto da 200 spire avvolte su un nucleo non ferromagnetico, di diametro 2 cm e lunghezza 10 cm.

La sezione del nucleo è pari a:

Usando μ = μ0, si ottiene:

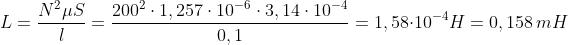
Esempio: Calcolare il numero di spire occorrente per avere L = 1 mH nel caso del solenoide del precedente esempio.

Il valore di N si ricava con la formula inversa :

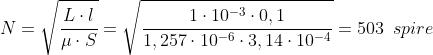
Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara