



Crescere richiede un'intera vita ma per diventarevecchi una notte è sufficiente
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!
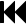

Massa
kilogrammo
kg
CAMPI MAGNETICI INDOTTI


Campo magnetico prodotto da
una spira circolare
Se il conduttore rettilineo descritto nella pagina precedente
viene avvolto in modo che formi una circonferenza di raggio
r, si ottiene una spira circolare, in cui il verso di percorrenza
della corrente può essere orario o antiorario (figura (a).
Le linee di forza del campo magnetico prodotto, che nel caso
del conduttore rettilineo si disponevano su piani tra loro
paralleli, si disporranno adesso su piani perpendicolari al
conduttore, non più paralleli tra loro, ma posti su direzioni
radiali, convergenti nel centro della spira. Immaginando di
tagliare la spira con un piano perpendicolare alla spira
stessa, si ottiene la rappresentazione di figura (b, in cui le
linee di forza sono linee chiuse attorno al conduttore, più
dense all’interno della spira e più rade all’esterno.
Man mano che ci si avvicina al centro della spira, la lunghezza delle linee di forza aumenta,
diventando infinita per quella centrale, rettilinea, ma che va immaginata come una linea
chiusa all’infinito.
Il verso delle linee di forza può ancora essere determinato con il palmo chiuso della mano
destra, orientando il pollice secondo il verso della corrente.

L’intensità del campo magnetico varia, a seconda del punto dello spazio considerato; il
valore maggiore lo si ha nel centro della spira, che è il punto che più risente dell’azione
combinata dei due conduttori; in tale punto l’intensità del vettore induzione magnetica
è pari a:
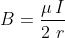
Induzione del campo
magnetico prodotto
da una spira circolare
Il campo magnetico risulta, quindi, tanto più intenso quanto maggiore è il valore della
corrente magnetizzante che l’ha prodotto e quanto minore è il raggio r della spira
(i conduttori risultano più vicini al punto considerato e, quindi, la loro azione magnetizzante
è maggiore); il valore di B è, inoltre, tanto più elevato quanto maggiore è la permeabilità
del mezzo, ossia quanto più facilmente il materiale magnetico si presta a essere magne-
-tizzato

Esempio: Calcolare la corrente che deve circolare in una spira di raggio 1,5 cm, in aria, per
produrre al suo interno un’induzione magnetica di 0,05 T
Utilizzando per la permeabilità il valore di quella del vuoto e ricavando la formula
inversa, si ottiene:

Il risultato ottenuto mostra che per creare un campo magnetico di valore apprezzabile
occorre impiegare correnti di valore molto elevato; a questo si può porre rimedio, come si
vedrà in seguito, aumentando il numero di spire in serie e usando materiali magnetici con
permeabilità magnetica molto maggiore di quella dell’aria.

Campo magnetico prodotto da un solenoide
Si considerino due spire accostate, percorse nello stesso senso dalla stessa corrente I
(come in figura A).
Osservando i versi delle linee di forza prodotte separatamente dalle due spire, si può
osservare che all’interno e all’esterno delle spire le linee di forza hanno lo stesso verso,
mentre nello spazio tra i conduttori hanno verso opposto. Dato che le spire sono uguali e
percorse dalla stessa corrente, è lecito affermare che i due contributi al campo risultante
saranno uguali e opposti e, quindi, l’intensità del campo sarà nulla nello spazio compreso
tra le spire.
Per ottenere un solenoide rettilineo occorre avvolgere più spire attorno a un supporto
(figura B), in modo che tutte le spire siano percorse dalla stessa corrente, nello stesso
senso. Le linee di forza del campo magnetico prodotto dal solenoide si svilupperanno sia
all’interno che all’esterno dello stesso, dando luogo alla configurazione indicata nella
figura B, simile a quella di un magnete permanente della stessa forma del solenoide.
Il campo magnetico avrà polarità N all’estremità del solenoide dove escono le linee di
forza ed S all’altro estremo (linee di forza entranti). Dato che il verso delle linee di forza
dipende da quello della corrente, ne consegue che invertendo il verso di percorrenza
della corrente nell’avvolgimento, si invertono le polarità del campo magnetico prodotto.

La soprastante espressione, pur non essendo stata dimostrata analiticamente, si può
giustificare intuitivamente, considerando che:
• l’intensità del campo magnetico è direttamente proporzionale alla permeabilità del
mezzo e all’intensità della corrente magnetizzante, così come avveniva per i campi
prodotti da un conduttore e da una spira;
• all’aumentare del numero di spire aumenta B, in quanto la corrente, percorrendo le
N spire, ripete per N volte la sua azione magnetizzante;
• l’intensità del campo magnetico è inversamente proporzionale alla lunghezza del
solenoide, in quanto all’aumentare di l diventa più lungo il tratto da magnetizzare
e, quindi, meno efficace l’azione della corrente.
Se le spire vengono avvolte attorno a un supporto chiuso su se stesso, di forma
circolare, si ottiene un solenoide toroidale (figura C), nel quale le linee di forza
sono tutte confinate all’interno delle spire. In questo caso le polarità N/S non sono più
evidenti, a meno che non si pratichi un’interruzione nel supporto (detta traferro), le
cui estremità costituiranno i poli N e S del magnete (figura D).
Il campo magnetico all’interno del solenoide si può ritenere costante e l’intensità
del vettore
è data da:
dove N è il numero di spire ed l è la lunghezza del solenoide.

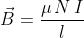

L’intensità del vettore può ancora essere calcolata con la formula [D1.5]; indicando con
r il raggio medio del toroide, la lunghezza l del solenoide sarà pari a quella della
circonferenza media e, quindi, il valore di
relativo alla linea di forza centrale sarà dato
da:



Induzione del campo magnetico
prodotto da un solenoide
toroidale
Dato che la differenza di lunghezza tra le varie linee di forza è trascurabile, si può
ritenere che il valore di
calcolato con la soprastante relazione, sia costante per tutti i
punti interni al toroide


Esempio : Su un solenoide toroidale, di raggio medio r = 10 cm, sono avvolte 100 spire
percorse dalla corrente I = 5 A. Calcolare il valore dell’induzione magnetica nei
due casi seguenti:
a) spire avvolte su un nucleo con permeabilità magnetica circa pari a quella del
vuoto;
b) spire avvolte su un nucleo con permeabilità pari a 1000 μo
Per entrambi i casi, possiamo utilizzae la stessa relazione:
Caso a
Caso b

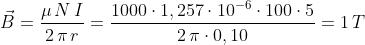
Come era logico attendersi, nel secondo caso il campo ottenuto ha un’induzione
magnetica di valore 1000 volte superiore rispetto al primo, a conferma dell’importanza
della permeabilità magnetica del materiale.

Esempio : Calcolare il numero di spire occorrente affinché all’interno di un solenoide
rettilineo avvolto su un nucleo di materiale avente μ = μ0, , di lunghezza 15 cm,
si crei un campo di induzione magnetica B = 0,01 T quando la corrente magnetiz-
-zante è pari a 20 A.
Se si ricava N dall’espressione conosciuta, si ha:



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





