Le persone che non soffrono mai non possono crescere né sapere chi sono

ELETTRONICA

… studiare, studiare ed ancora studiare, è il solo modo di capire quanto possa essere grande sia la propria ignoranza!

Massa

kilogrammo

ELETTROMAGNETISMO - CIRCUITI MAGNETICI

OBIETTIVI:

Al termine di questa nuova sezione, i lettori dovranno: 1. conoscere le grandezze magnetiche e i loro legami; 2. conoscere le principali leggi dell’elettromagnetismo e saperle associare ai relativi fenomeni; 3. conoscere il bipolo “induttore” e il suo comportamento circuitale; 4. conoscere i fenomeni che avvengono durante il periodo transitorio di magnetizzazione e smagnetizzazione di un induttore; 5. saper risolvere una rete elettrica di media complessità contenente un induttore, durante il periodo transitorio.

RICHIAMI DI MAGNETISMO

• Campo magnetico. Una regione di spazio è sede di un campo magnetico se un magnete di prova, posto in un qualsiasi punto di quello spazio, è soggetto a forze che tendono a farlo ruotare fino a disporlo in direzione parallela al campo magnetico. • Magnete di prova. Per “magnete di prova” si intende un ago magnetico (come quello della bussola), ossia una piccola calamita, di forma stretta e allungata, che può ruotare intorno a un perno centrale; esso è provvisto, come tutti i magneti, di due poli magnetici, indicati con N (nord) e S (sud). • Origine del campo magnetico. Un campo magnetico è generato sempre da cariche elettriche in movimento. Nel caso dei magneti permanenti il movimento di cariche è dovuto al moto degli elettroni degli atomi del magnete, mentre nel caso degli elettro- -magneti è la corrente elettrica circolante entro un filo conduttore che produce il campo magnetico. 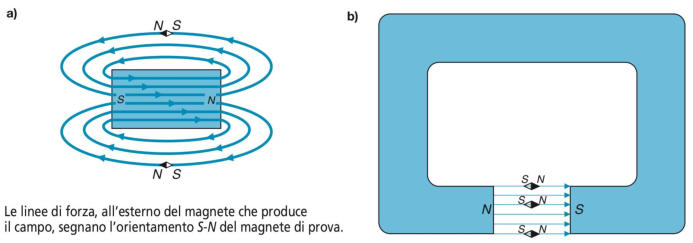• Linee di campo. Dette anche linee di forza, sono linee orientate che consentono di rappresentare graficamente l’azione del campo magnetico. Un magnete di prova, posto in un punto del campo magnetico, sotto l’azione della forza magnetica si orienta sempre nella direzione tangente alla linea di forza in quel punto, mentre il verso della linea di forza va dal polo S al polo N del magnete di prova. Nelle figure (a) e (b) sono rappresentate le linee di forza in due casi tipici: barra magnetica rettangolare e magnete con polarità contrapposte. • Polarità di un magnete. Le polarità di un magnete permanente o di un elettroma- -gnete sono determinate dal verso delle linee di forza: all’esterno del magnete le linee di forza escono dal polo N ed entrano nel polo S (figure A) e B)) • Poli magnetici isolati. Non è possibile avere un magnete con una sola polarità, a differenza di quanto accade per le cariche elettriche, che possono essere positive o negative. Dividendo in due parti una calamita, ciascuna parte formerà un magnete, dotato di entrambe le polarità

Nella sottostante figura è rappresentata una circonferenza trigonometrica, avente raggio unitario, divisa in quattro quadranti dagli assi cartesiani x e y.

FUNZIONI TRIGONOMETRICHE

Preso un punto P sulla circonferenza, con –– OP = 1 in quanto corrispondente al raggio, e individuati i punti A e C sull’asse x, B sull’asse y, T sulla retta t1 e D sulla retta t2, si definiscono le seguenti funzioni trigonometriche aventi per argomento l’angolo α:

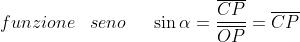
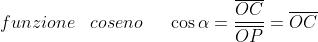
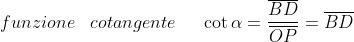
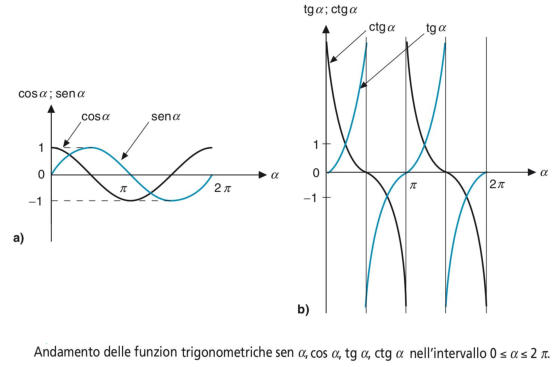
L’andamento delle funzioni trigonometriche al variare di α è indicato nelle figurr sottostanti a) e B), relativamente all’intervallo da zero a 2π, corrispondente a un giro del punto P sulla circonferenza.

Nella tabella sono riportati i valori delle quattro funzioni per alcuni valori particolari dell’angolo

Gradi

Radianti

sen

cos

ctg

1/2

180

-1

270

-1

360

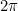
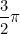
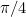
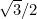
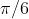
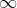
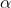
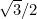
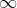
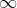
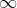
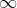
Tra le quattro funzioni trigonometriche introdotte valgono le seguenti identità trigonometriche:

Relazioni tra i lati di un triangolo rettangolo

In un triangolo rettangolo di cateti a e b e ipotenusa c valgono le seguenti relazioni, ricavabili dalla similitudine tra il triangolo dato e quello corrispondente sul cerchio trigonometrico:

Le formule scritte corrispondono alle seguenti regole: • la misura di un cateto è uguale a quella dell’ipotenusa per il seno dell’angolo opposto al cateto; • la misura di un cateto è uguale a quella dell’ipotenusa per il coseno dell’angolo compreso tra cateto e ipotenusa; • la misura di un cateto è uguale a quella dell’altro cateto per la tangente dell’angolo opposto al primo . Valgono anche tutte le relazioni ricavabili come formule inverse da quelle riportate

Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara