Diventare vecchi è obbligatorio - crescere è opzionale

ELETTRONICA

… studiare, studiare ed ancora studiare, è il solo modo di capire quanto possa essere grande sia la propria ignoranza!

Massa

kilogrammo

FENOMENI TRANSITORI NEI CIRCUITI CAPACITIVI

Si esaminerà, in questo capitolo, il comportamento di un circuito capacitivo durante l’intervallo di tempo in cui il condensatore scambia energia elettrica con il resto del circuito a cui è collegato. Durante questo tempo la carica elettrica sulle armature del condensatore varia: quando essa aumenta si parla di transitorio di carica, in caso contrario di transitorio di scarica. Il termine “transitorio” indica che il fenomeno non è permanente, ma temporaneo e, quindi, cessa dopo un certo tempo. Questo avviene nelle reti in cui sono presenti generatori elettrici di tipo continuo, che impongono tensioni costanti nel tempo: quando i condensatori sono completamente carichi, le d.d.p. ai loro capi raggiungono i valori imposti dal regime di funzionamento del circuito e la circolazione di corrente nei lati capacitivi della rete cessa. Così non avviene con generatori in corrente alternata

Transitorio di carica di un condensatore

Si consideri la figura a sinistra, un circuito formato da un generatore di tensione continua, di f.e.m. E., collegato a un condensatore di capacità C, supposto inizialmente scarico; un interruttore permette di collegare il condensa- -tore al generatore. Il resistore R rappresenta la resistenza complessiva di tutto il circuito.

Alla chiusura dell’interruttore (figura a) inizia il processo di carica del condensatore e una corrente i fluisce nel circuito esterno; sul condensatore inizia ad accumularsi una carica elettrica q e tra le armature comincia a manifestarsi una tensione vc che agisce in opposizione alla f.e.m. E e, quindi, si oppone anche alla corrente di carica. Quando il condensatore sarà completamente carico (figura b), la tensione sullo stesso sarà pari alla E, la corrente si annullerà e il condensatore avrà accumulato la carica finale Q = CE.

Per studiare quello che avviene durante il periodo di carica, si consideri l’equazione di Kirchhoff alla maglia, per il circuito di figura (a:

da cui si ricava la corrente di carica:

L’esame di questa relazione, consente di fare un’importante osservazione: all’aumentare della tensione vc, essendo E costante, il numeratore di detta relazione diminuisce e, quindi, diminuisce anche la corrente; pertanto la carica di un condensatore avviene con corrente variabile nel tempo e man mano decrescente. Dato che, in realtà, sono gli elettroni che si spostano da un’armatura all’altra, con verso opposto alla corrente, si può dire che il flusso di elettroni durante il processo di carica diventa sempre meno intenso. Si consideri ora un intervallo di tempo Δt, scelto sufficientemente piccolo da poter ritenere costante la corrente per tutto l’intervallo (è, ovviamente, un’approssimazione, dato che la corrente varia nel tempo); in tale intervallo vi sarà una variazione di carica elettrica Δq sulle armature del condensatore, legata alla corrente dalla relazione:

La variazione di carica comporterà una variazione della tensione sul condensatore, data da

Anche l’esame di questa relazione, consente di fare un’importante osservazione: supponendo di dividere la durata del fenomeno di carica in tanti intervalli di tempo uguali tra loro, nella suddetta relazione, il rapporto Δt/C rimane costante e, quindi, al diminuire della corrente, si riducono anche le variazioni della tensione; si deduce pertanto che la carica del condensatore avviene con variazioni sempre minori della tensione ai suoi capi, ossia la tensione sul condensatore andrà man mano aumentando, ma con incrementi sempre più piccoli. Dato che la corrente tende a zero quando nella relazione, vc tende ad E, anche la Δvc tenderà a zero e la tensione vc tenderà a un valore costante, dato appunto dalla f.e.m. E.

Per trovare la funzione matematica vc = f (t) che descrive la legge di variazione della tensione, occorre risolvere l’equazione che si ottiene dalla sostituendo in essa l’espressione di i ricavata dall’ultima relazione; si ha:

Nella soprastante equazione compaiono gli incrementi finiti delle grandezze vc e t, ossia variazioni piccole quanto si vuole, ma di valore ben definito (per esempio, nel caso di Δt, un decimo di secondo, un centesimo di secondo, un millesimo di secondo ecc.); per applicare i metodi dell’analisi matematica si devono considerare, invece, gli intervalli infinitesimi dt e dvc , a cui non si possono attribuire dei valori. Procedendo in questo modo, la soprastante equazione diventa:

espressione che si chiama equazione differenziale, la cui soluzione esula dai nostri scopi. Ritornando alle considerazioni fatte prima, si può comunque affermare che la curva che descrive l’andamento della tensione vc nel tempo dovrà possedere i seguenti requisiti: • valore iniziale nullo (condensatore inizialmente scarico); • andamento crescente nel tempo (la tensione sul condensatore aumenta al procedere della carica); • incrementi della tensione man mano più piccoli; • tendenza a raggiungere un valore finale ben definito (la tensione sul condensatore non aumenta fino all’infinito, ma tende al valore E).

La legge matematica che soddisfa le condizioni indicate e che è soluzione dell’equazione differenziale è la curva esponenziale crescente della figura a lato; essa rappresenta la curva di carica del condensatore collegato a un generatore di tensione costante e corrisponde alla funzione:

dove Vf = E è la tensione finale e τ è la costante di tempo del sistema, da cui dipende la durata del fenomeno di carica. L’analisi del grafico della soprastante figura, mostra che, in teoria, il processo di carica di un condensatore, come tutti i processi che avvengono in maniera esponenziale, dura per un tempo infinito, dato che la tensione vc si avvicina sempre più a quella finale, senza tuttavia mai raggiungerla (in matematica si dice che tende asintoticamente). In pratica, il processo di carica si considera concluso quando la tensione effettiva si discosta da quella teorica finale di uno scarto percentuale prefissato. Normalmente si considera uno scarto dell’1% e il tempo corrispondente viene detto tempo di assestamento (in questo caso all’1%)

Dalle pagine precedenti abbiamo

espressione che giustifica l’affermazione qualitativa che considera concluso il fenomeno di carica dopo 4÷5 volte la costante di tempo. Il ruolo della costante di tempo è fondamentale in questi processi: la durata del transitorio di carica è direttamente proporzionale alla costante di tempo del circuito di carica, aumentando con il suo valore.

Per quanto riguarda l’andamento della corrente si può dire che: • nell’istante iniziale del processo di carica, essendo ancora vc = 0, la corrente nel circuito assume il valore massimo; ponendo vc= 0 nella i=(E-vc)/R, si ricava il valore iniziale della corrente: • all’aumentare della tensione sul condensatore la corrente diminuisce; • quando il processo di carica è concluso, la corrente è nulla (If= 0); in teoria, dato che la tensione non arriva mai al valore finale, anche la corrente non arriverà mai a zero. 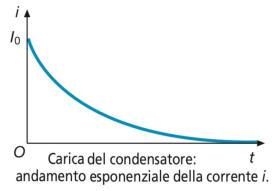La funzione che descrive l’andamento nel tempo della corrente è ancora di tipo esponenziale, ma decrescente, data da:

il cui grafico è rappresentato da

Espressione della costante di tempo È possibile ricavare l’espressione della costante di tempo del circuito R-C partendo dalla seguente definizione: la costante di tempo è pari al tempo necessario per caricare il condensatore alla tensione E del generatore, supponendo che la carica avvenga con corrente costante, pari a quella iniziale. In questo caso la carica finale, data dal prodotto Q = CE, sarà anche pari a Q = I0 τ, dove I0 = E/R; uguagliando i secondi membri si avrà:

La formula mostra che la costante di tempo è direttamente proporzionale al valore dei parametri R e C del circuito e, quindi, aumenta con essi. Considerando che τ è legata alla durata del processo di carica, la dipendenza può essere spiegata nel seguente modo: all’aumentare della capacità cresce anche la carica finale e quindi occorre più tempo per accumularla sulle armature del condensatore; invece all’aumentare della resistenza diminuisce la corrente di carica e quindi aumenta il tempo necessario per compiere il processo di carica.

Caso del condensatore inizialmente carico Se il condensatore è inizialmente carico con tensione V0 e tende ad arrivare alla tensione finale Vf, la legge di variazione della tensione è data da:

rappresentata da:

Si può verificare che i valori estremi sono rispettati: • per t = 0 si ha e vc= Vf+ V0− Vf= V0 • per t ∞ si ha e vc= Vf L’espressione sopra descritta può essere considerata una formula generale, valida ogni volta che la tensione varia esponenzialmente da un valore iniziale a uno finale. Da essa si ricava anche l’espressione ponendo V0 = 0

Una formula analoga può essere scritta per la corrente:

Esempio:Un condensatore di capacità C = 10 μF, inizialmente scarico, viene caricato da un generatore con f.e.m. E = 200 V, tramite un circuito che presenta una resistenza di 1 kΩ. Calcolare la costante di tempo, la corrente iniziale di carica, il tempo di assestamento all’1% e l’energia elettrostatica accumulata dopo tale tempo.

Con le formule già espresse, si calcolano i valori della costante di tempo e del tempo di assestamento:

Al tempo di assestamento la tensione sul condensatore è pari al 99% di quella finale, ossia uguale a :

e quindi l’energia sarà pari a:

La corrente iniziale di carica è data da:

Esempio: Per il condensatore dell’esempio precedente calcolare la tensione sul condensatore e la corrente nel circuito al tempo t1 = 30 ms e il tempo t2 necessario affinché la tensione arrivi al valore V2 = 60 V

Dato che il condensatore è inizialmente scarico, la tensione e la corrente variano con le leggi conosciute già espresse; sostituendo il valore di t1 si ha:

Per calcolare la tensione V2 bisogna risolvere la seguente equazione con incognita t2, che deriva dall’applicazione della nota relazione:

Usando la formula, per il calcolo del tempo si ha:

Esempio: Un condensatore di capacità C = 20 nF, inizialmente carico con tensione 5 V, viene ulteriormente caricato fino alla tensione di 25 V. Il circuito di carica ha una costante di tempo di 20 ms. Calcolare la resistenza del circuito, la carica iniziale, la carica finale, l’energia che il circuito di carica ha fornito al condensatore, la tensione sul condensatore nell’istante t1 = 2τ

La resistenza del circuito di carica è data da:

I valori iniziale e finale della carica elettrica sono legati ai corrispondenti valori di tensione:

Durante il transitorio di carica l’energia elettrostatica immagazzinata dal condensatore aumenta: l’incremento di energia nel condensatore sarà pari all’energia che il circuito esterno gli ha fornito:

Il calcolo della tensione all’istante t1 si esegue applicando la relazione:

Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara