



Ho sempre trattato le persone con i guanti... da Boxe!
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!


Massa
kilogrammo
kg
CAPACITA’ DI UN CONDENSATORE




Capacità di un condensatore
Un condensatore, dal punto di vista del comportamento
circuitale, è un bipolo in grado di accumulare carica elettrica
sulle sue armature quando viene caricato da un circuito
esterno e di conservarla anche dopo essere stato scollegato.
Dato che il processo di carica continua fino a quando non si
raggiunge la tensione imposta dal circuito esterno (compa-
-tibilmente con la tensione massima sopportabile dal
condensatore), è evidente che la quantità di carica
accumulata sarà direttamente proporzionale alla tensione,
secondo la relazione:

Si definisce capacità del condensatore il rapporto:

Ponendo V = 1 V nella soprastante espressione, si ha che C e Q coincidono numericamente
e quindi si può affermare che:
la capacità di un condensatore rappresenta la carica elettrica accumulata sul
condensatore stesso per unità di tensione applicata.
La capacità si misura in farad (F): il valore di 1 F indica che il condensatore immagazzina la
carica di 1 C per ogni volt di tensione applicata.
Dato che i condensatori reali hanno capacità molto inferiori a 1 F, in pratica si usano i
sottomultipli microfarad (1 μF = 1 × 10–6 F), nanofarad (1 nF = 1 × 10–9 F) e picofarad
(1 pF = 1 × 10–12 F).
Dall’ultima espressione si ottiene la formula inversa:

che consente di ricavare la tensione sul condensatore.


a) Un condensatore accumula la carica Q = 100 μC con V = 10 V. Calcolare la sua
capacità in microfarad.
b) Un condensatore di capacità 5 μF viene caricato con tensione 100 V. Calcolare la
caricaimmagazzinata.
c) Calcolare la tensione occorrente per avere una carica di 100 nC in un condensatore di
capacità 0,005 μF.
Per il calcolo a) si ha:
Esercizio:

Per il calcolo b) si ha:


Per il calcolo c) si ha:

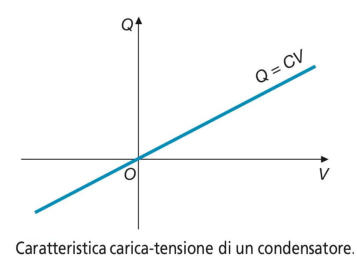
L’espressione Q=C V, essendo C costante, può essere intesa come l’equazione di una retta
passante per l’origine (vedi sottostante figura ); essa costituisce l’equazione caratteristica
del bipolo condensatore.
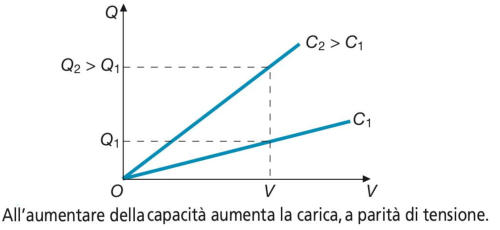
All’aumentare della capacità C la carica, a parità di tensione, aumenta; nella figura che
segue sono riportate le caratteristiche, limitate ai semiassi positivi, di due condensatori
di diversa capacità.
Capacità del condensatore piano
L’espressione C=Q/V è valida per un qualsiasi condensatore, in quanto discende
dalla definizione di capacità. Nel caso di un condensatore piano è possibile ricavare
un’altra espressione della capacità, in funzione delle caratteristiche costruttive del
componente:

dove A è la superficie delle armature, d è la loro distanza ed ε è la costante dielettrica del
materiale isolante interposto, pari al prodotto:



tra la costante dielettrica assoluta del vuoto εo(detta anche permettività assoluta) e la
costante dielettrica relativa εr dell’isolante, dipendente dal tipo di materiale dielettrico.

Essendo , la soprastante espressione diventa:
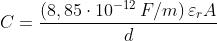
Esprimendo A in metri quadrati e d in metri, l’espressione fornisce il valore di C in farad.
La costante dielettrica relativa gioca un ruolo importante nella costruzione di condensatori
di elevata capacità: usando materiali con elevati valori di εr aumenta la capacità del
condensatore, a parità di dimensioni geometriche. ( si rimanda al relativo capitolo delle
Tecnologie).
Per la maggior parte dei dielettrici i valori di εr variano da 1 a 10, ma vi sono anche
materiali particolari, come il titanato di bario, con costante dielettrica relativa di qualche
migliaio.
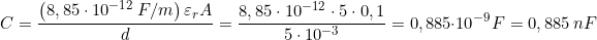

Esempio: Calcolare la capacità di un condensatore piano avente A = 0,1 m2, d = 5 mm,
εr = 5
Mediante l’ultima espressione, si ricava immediatamente:

Energia elettrostatica
Durante il processo di carica il generatore esterno fornisce al condensatore energia
elettrica, che resta immagazzinata nel condensatore stesso sotto forma di energia
potenziale elettrostatica.
Per calcolare la quantità di energia accumulata in un condensatore di capacità C si
consideri il sottostante grafico, dove V e Q sono rispettivamente i valori finali della
tensione e della carica elettrica
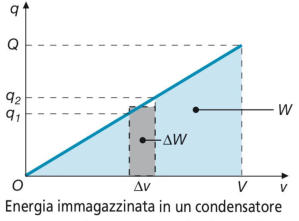
Quando il condensatore subisce una variazione di tensione Δv, la carica si incrementa dal
valore q1 al valore q2.
Indicando con il valore medio della carica nell’intervallo considerato,
l’incremento di energia immagazzinata nel condensatore sarà pari a:
e corrisponderà all’area del rettangolo evidenziato nella figura.
Durante tutto il processo di carica la tensione passerà da zero a V e la carica da
zero a Q; l’energia totale sarà data dalla somma di tutti gli incrementi:
e corrisponderà all’area del triangolo sotteso al segmento di retta del grafico di figura,
area data da:

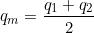

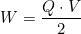
che con le opportune sostituzioni
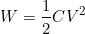

Da quest’ultima formula si deduce che, a parità di tensione applicata, l’energia
immagazzinata in un condensatore è direttamente proporzionale alla sua capacità.

Esempio:Un condensatore di capacità C = 20 μF viene caricato con tensione V = 100 V;
calcolare la carica e l’energia accumulate.
Usando le soprastanti formule, si ha
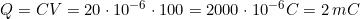

Allo stesso risultato si perviene calcolando l’energia con
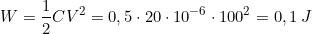



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





