Le delusioni dell'età matura seguono le illusioni della gioventù.

ELETTRONICA

… studiare, studiare ed ancora studiare, è il solo modo di capire quanto possa essere grande sia la propria ignoranza!

Massa

kilogrammo

GRANDEZZE CON ANDAMENTO ESPONENZIALE

Grandezze con andamento esponenziale nel tempo

Andamento esponenziale crescente Molti processi fisici (per esempio, il riscaldamento di un corpo, la carica di un condensatore ecc.) avvengono, sotto determi- -nate ipotesi, secondo una legge matematica descritta dalla funzione: [a] dove: • y è il valore della grandezza fisica in esame all’istante t (variabile dipendente della funzione); • t è il tempo (variabile indipendente della funzione); • Yf è il valore finale della grandezza y; • τ è la costante di tempo, il cui ruolo nell’evoluzione della grandezza y verrà definito nel seguito della trattazione; • e = 2,71828… è la base dei logaritmi naturali o neperiani; • è una funzione esponenziale, con esponente negativo e base e.

I valori assunti dalla soprastante funzione, in corrispondenza di determinati valori del tempo, sono riportati nella tabella che segue.

Per il calcolo dell’esponenziale basta usare una normale calcolatrice provvista di tale funzione.

Valori tipici della funzione [a]

% del valore finale

0,368

0,632

63,2

0,135

0,865

86,5

0,0498

0,950

0,0183

0,982

98,2

4,6

0,010

0,990

0,00674

0,993

99,3

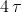
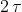
Il soprastante grafico mostra l’andamento di y in funzione del tempo come riportato nella figura. Esaminando il grafico e la tabella si possono fare le seguenti considerazioni: • la grandezza y parte da un valore iniziale nullo e tende a un valore finale Yf,senza però mai raggiungerlo; nel linguaggio matematico Yf rappresenta l’asintoto orizzontale della funzione e i valori di y tendono asintoticamente a Yf; • in teoria la grandezza y non arriva mai a un valore costante; in pratica la sua evoluzione si considera conclusa quando lo scostamento rispetto al valore finale diventa minore di un valore prefissato, normalmente pari all’1%; • particolarmente significativo diventa il valore 4,6τ, per il quale si ha y = 0,99Yf (scostamento pari a 1%); il tempo Ta = 4,6τ è detto tempo di assestamento e rappresenta la durata pratica del processo di crescita esponenziale della grandezza y; esso è direttamente proporzionale al valore della costante di tempo, dalla quale dipende, pertanto, tale durata; • l’aumento della grandezza y avviene con incrementi sempre decrescenti; questo si nota facilmente dalla tabella: nel primo intervallo (da 0 a 1τ) la y aumenta da 0 a 0,632Yf (incremento del 63,2%), mentre nel secondo intervallo (da 1τ a 2τ) cresce dal 63,2% all’86,5% del valore finale (incremento del 23,3%) e successivamente sempre meno.

Calcolo del valore di y, noto t Questa operazione si esegue direttamente usando l’espressione dell’andamento esponenziale crecente, come riportato nell’esempio seguente. Esempio 1: Conoscendo τ = 2 s e Yf= 10, calcolare il valore y1all’istante t1= 5 s. Si ha:

Calcolo del valore di t, noto y Questa operazione è più complessa della precedente, dato che t compare nell’espressione dell’esponente e non in modo esplicito. Si può ricavare una formula diretta per il calcolo del tempo, operando nel seguente modo:

A questo punto, per ricavare l’esponente, si ricorre alla funzione inversa dell’esponenziale, ossia al logaritmo naturale ln (funzione anch’essa presente sulle comuni calcolatrici), ottenendo:

ed infine

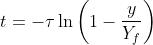
Esempio 2 Con i dati del precedente esempio calcolare dopo quanto tempo la grandezza y assume il valore 6. Applicando la soprastante formula con y1= 6, si calcola il tempo t1 richiesto:

Andamento esponenziale decrescente L’andamento nel tempo di una grandezza y che parte da un valore iniziale Yo e tende esponenzialmente a zero è descritto dalla funzione:

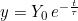
I valori assunti dalla suddetta funzione, in corrispondenza di determinati valori del tempo, sono riportatinella seguente tabella:

Valori tipici della funzione [B]

% del valore iniziale

100

0,368

36,8

0,135

13,5

0,0498

4,98

0,0183

1,83

4,6

0,010

0,10

0,00674

0,674

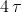
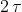
[B]

Il grafico che mostra l’andamento di y in funzione del tempo è quello sottostante:

Dall’esame del grafico e della tabella scaturiscono le seguenti considerazioni: • la grandezza y parte dal valore iniziale Y0e tende a un valore finale nullo, senza però mai raggiungerlo; nel linguaggio matematico si dice che y tende asintoticamente a zero; • in teoria la grandezza y non si annulla mai; in pratica la sua evoluzione si considera conclusa dopo il tempo di assestamento Ta= 4,6τ, quando il suo valore è pari all’1% di quello iniziale; • la diminuzione della grandezza y avviene con decrementi sempre più piccoli; questo si nota facilmente dalla tabella: nel primo intervallo (da 0 a 1τ) la y diminuisce da Y0 a 0,368Y0 (decremento del 63,2%), mentre nel secondo intervallo (da 1τ a 2τ) diminuisce dal 36,8% al 13,5% del valore iniziale (decremento del 23,3%) e successivamente sempre meno

Calcolo del valore di y, noto t Questa operazione si esegue direttamente usando l’espressione dell’andamento esponenziale decrescente, come riportato nell’esempio seguente. Esempio: Conoscendo τ = 0,1 s e Y0 = 100, calcolare il valore y1 all’istante t1 = 0,35 s. Si ha:

Calcolo del valore di t, noto y In questo caso l’incognita t compare nell’espressione dell’esponente e non in modo esplicito. Si può ricavare una formula diretta per il calcolo del tempo, operando nel seguente modo:

ed infine:

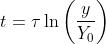
Un ulteriore esempio: Con i dati del precedente esempio calcolare dopo quanto tempo la grandezza y assume il valore 70.

Applicando la soprastante formula con y1 = 70, si calcola il tempo t1 richiesto:

Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara