



Le donne piangono il giorno del matrimonio. Gli uomini dopo
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!


Massa
kilogrammo
kg
TEOREMA DI MILLMANN E SOVRAPPOSIZIONE DEGLI EFFETTI




Teorema di Millmann
Il teorema di Millmann è un mezzo molto efficace per
risolvere le reti binodali, ossia aventi soltanto due nodi,
consentendo di calcolare in modo immediato la tensione
tra i due nodi, nota la quale è facile risalire alle correnti
nei lati.
Si consideri il circuito di figura, in cui il nodo B, collegato a massa, si assume come
riferimento a potenziale zero (VB= 0). Scrivendo l’equazione al nodo A si ottiene:




Ricavando si ottiene:

Generalizzando la formula vista nel capitolo precedente per una rete binodale con l lati
si può scrivere:

dove n è il numero dei lati contenenti bipoli attivi di tensione con f.e.m Ei e conduttanze Gi
, m è il numero dei lati con bipoli attivi di corrente con correnti impresse I0j e l è il numero
totale dei lati, le cui conduttanze Gq comprendono anche le Gi.
La regola generale si esprime pertanto nel seguente modo:
la tensione tra i nodi di una rete binodale è data da un rapporto, il cui denominatore è la
somma aritmetica delle conduttanze di tutti i lati, mentre il numeratore si calcola come
somma algebrica (con segno) delle correnti di cortocircuito GiEi dei bipoli attivi di tensione
più la somma algebrica delle correnti impresse dai bipoli attivi di corrente

I termini della prima sommatoria al numeratore sono positivi se il morsetto “+” della
relativa f.e.m. corrisponde al primo nodo (A per la tensione VAB) e negativi in caso
contrario. I termini della seconda sommatoria al numeratore sono positivi se le correnti
impresse sono dirette verso il primo nodo e viceversa.

Della rete in figura calcolare la tensione VAB e le correnti nei lati.

Le conduttanze dei singoli lati sono date da :



Applicando il teorema di Millmann, si ha:

Per decidere il verso delle correnti occorre osservare :

•
VAB > 0 e quindi VA> VB; nel resistore R2 la corrente andrà da A verso B;
•
VAB < E1 e pertanto il lato E1-R1-R4 si comporterà da generatore, con corrente
uscente dal “+” di E1;
•
VAB < E3 e quindi anche il lato E3-R3-R5 si comporterà da generatore, con corrente
uscente dal “+” di E3.
Eseguendo i calcoli, si ha:

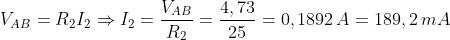

Per controllo si può verificare il primo principio di Kirchhoff al nodo A:

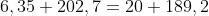

La lieve differenza nei valori deriva dalle approssimazioni di calcolo

Nel circuito in figura calcolare la corrente I4 applicando il teorema di Millmann.


Per eliminare il nodo C si trasforma il bipolo attivo parallelo I02-R2 nell’equivalente bipolo
serie E2-R2, con E2= I02 R2= 4 × 10 = 40 V. Si ottiene il sottostante circuito (a).
Il lato di sinistra comprende due resistori in serie e due bipoli attivi con f.e.m. agenti
nello stesso senso; può essere ridotto come mostrato nella figura (b), dove:

ed applicando il teorema di Millmann, si ottiene:

e quindi:
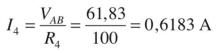
Sovrapposizione degli effetti
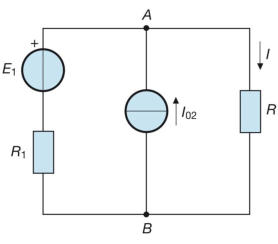
Si consideri il sottostante circuito, del quale si vuole calcolare la corrente I.
Applicando il teorema di Millmann si ricava la tensione VA
Ponendo :
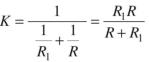
la soprastante espressione di Vab, diviene:

La corrente è data:
Quest’ultima espressione mostra che la corrente I è data dalla somma di due termini;
precisamente:
•
la corrente dovuta al solo generatore di tensione, supponendo nulla la
corrente I02 impressa dal generatore di corrente;
•
la corrente dovuta al solo generatore di corrente, supponendo nulla la
f.e.m. E1 del generatore di tensione.
Le precedenti osservazioni consentono di individuare il seguente metodo di calcolo
della corrente I:
•
si annulla la corrente I02, sostituendo al generatore di corrente un circuito aperto
ideale della sottostante figura (a e si determina la corrente I′ dovuta al generatore di
tensione;
•
si annulla la f.e.m. E1 , sostituendo al generatore di tensione un cortocircuito ideale
della figura (b e si determina la corrente I′′ dovuta al generatore di corrente;
•
si calcola la corrente effettiva I sommando, tenendo conto dei versi di percorrenza,
i due contributi I′ e I′′



Effetto della f.e.m E1
Effetto della corrente impressa I02
La regola esposta corrisponde all’applicazione di un principio generale, detto di
sovrapposizione degli effetti, valido per tutti i sistemi fisici lineari, non solo per quelli
elettrici. Esso consente di ricavare la corrente o la tensione di un qualsiasi bipolo di
una rete lineare scomponendo il circuito complessivo in tanti circuiti elementari, in
ognuno dei quali agisce un solo generatore, in quanto vengono disattivati tutti gli altri.
La regola generale per la sua applicazione è quindi la seguente:
•
data una rete lineare contenente n bipoli attivi (di corrente o di tensione) di cui si
vuole calcolare una grandezza elettrica (tensione o corrente) in un generico punto
della rete, si scompone il circuito in n circuiti parziali, in ognuno dei quali agirà un
solo bipolo attivo, avente funzione di generatore in quanto rimane l’unico compo-
-nente in grado di fornire energia elettrica al resto della rete;
•
ogni circuito parziale si ricava dalla rete iniziale disattivando tutti i bipoli attivi
meno uno, dove per “disattivazione” s’intende la sostituzione dei bipoli attivi di
corrente con circuiti aperti ideali (corrente impressa I0= 0) e la sostituzione dei
bipoli attivi di tensione con corto circuiti ideali (tensione interna E = 0);
•
si calcola la grandezza elettrica incognita in ognuno dei circuiti parziali; i vari
risultati ottenuti sono da intendere come i contributi dei vari generatori alla
grandezza incognita effettiva;
•
si sommano algebricamente gli n risultati ottenuti, tenendo conto dei segni dei
risultati parziali; più specificamente, occorre tener conto dei versi delle correnti
parziali e delle polarità delle tensioni parziali, a seconda dei casi.
Questo metodo si presta, in genere, alla risoluzione parziale di una
rete, quando è richiesto il calcolo di una determinata corrente o
tensione. La sua applicazione alla risoluzione totale, che si basa
sempre sulla procedura descritta precedentemente, risulta
normalmente piuttosto onerosa, dato che prevede la risoluzione
completa di n circuiti, ognuno con un solo generatore.
È utile osservare che la sovrapposizione degli effetti non è
applicabile a reti non lineari, ossia aventi anche un solo bipolo
con parametri non costanti al variare delle grandezze elettriche.
Si consideri, per esempio, il semplice circuito a destra, per il quale
si suppone che il resistore abbia una resistenza R variabile con la
tensione.
Ipotizzando che R valga 50 Ω con tensione 50 V e 80 Ω con tensione di 100 V, la corrente
effettiva sarà pari a 100/80 = 1,25 A, in quanto nelle reali condizioni di funzionamento la
resistenza è 80 Ω; l’applicazione della sovrapposizione degli effetti porterebbe invece a
due contributi di corrente pari ognuno a 50/50 = 1 A e, quindi, a una corrente di 2 A,
diversa da quella reale.
Inapplicabilità della
sovrapposizione
degli effetti


Determinare, in valore e verso, la corrente nel resistore R4 della rete in figura.
La rete comprende tre bipoli attivi, due di tensione e uno di corrente. Per applicare il
principio di sovrapposizione degli effetti bisogna risolvere i circuiti parziali riportati nelle
figure a) e b) e c), in cui le correnti parziali hanno i versi segnati, dipendenti dalle
polarità dei generatori.
Applicando la legge di Ohm e la regola del partitore di corrente si calcolano i tre
contributi alla corrente I4:



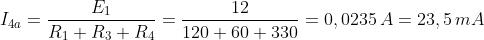
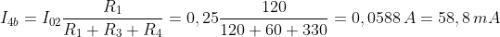
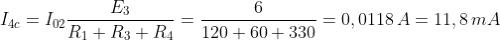
La corrente totale avrà il verso di I4b e di I4c, in quanto prevalenti rispetto a I4a, e il
suo valore sarà pari a:


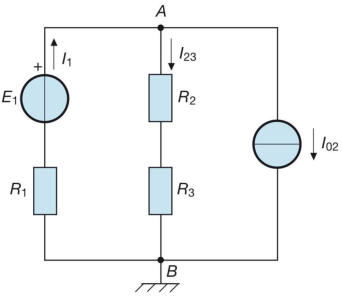
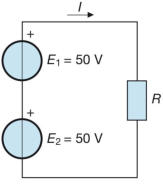
Calcolare la corrente I2 e il potenziale di B rispetto a massa nel circuito di figura:

Il circuito è disegnato in modo un po’ diverso dall’usuale, con le notazioni tipiche dei
circuiti elettronici. Si deve intendere che tra il punto A e massa è applicato un generatore
di tensione ideale con E1= 10 V, mentre tra il punto B e massa agisce un generatore
ideale di corrente di valore 100 mA.
I due circuiti parziali sono riportati nelle sottostanti figure a) e b):




Risolvendo i due circuiti, si ha:

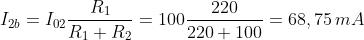
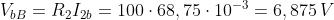
Dato che entrambi i contributi, per ambedue le grandezze, hanno lo stesso verso, la
corrente e la tensione richieste sono date da:
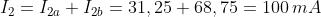

Si può notare che il potenziale di B rispetto a massa è esattamente uguale alla tensione
applicata al punto A: questo significa che il generatore di tensione funziona a vuoto e,
infatti, tutta la corrente I02 = 100 mA fluisce nella resistenza R2.


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





