



La donna che fa godere l'uomo è naturale, ma l'uomo che fa godere la donna... è talento.
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!


Massa
kilogrammo
kg
METODI DI RISOLUZIONE DELLE RETI ELETTRICHE LINEARI


In questo capitolo verranno presentati alcuni metodi di
risoluzione delle reti lineari, formate cioè dalla connessione
di bipoli tutti lineari, sia di tipo attivo che passivo.
La risoluzione di una rete contenente un numero l di lati
comporta, in generale, il calcolo della corrente e della
tensione per ogni lato; pur essendo molteplici i casi che
possono presentarsi, è possibile distinguere due categorie
di problemi; precisamente:
• casi in cui è richiesta la risoluzione completa della rete e
quindi il calcolo di l correnti e di l tensioni, per effettuare il
quale sono necessarie 2l equazioni, di cui l sono rappresen-
-tate dalle equazioni caratteristiche Vi= f (Ii) dei singoli lati;
• casi in cui è richiesta la risoluzione parziale della rete,
ossia il calcolo della tensione e della corrente in uno o più
lati, senza curarsi del resto della rete, che può anche subire
trasformazioni equivalenti durante la risoluzione.
Applicazione dei principi di Kirchhoff
L’applicazione dei due principi di Kirchhoff, introdotti nelle precedenti pagine, consente
di effettuare la risoluzione completa di una rete lineare, ossia di scrivere le l
equazioni che, unite alle l equazioni caratteristiche dei lati, permettono il calcolo
delle tensioni e delle correnti incognite. Dal sistema completo di 2l equazioni è facile
passare al sistema ridotto, detto sistema di Kirchhoff, scrivendo le equazioni dei
singoli bipoli solo in funzione delle correnti, in modo da avere un sistema lineare di l
equazioni contenenti le l correnti incognite, una per lato.
Indicando con n il numero dei nodi, la scrittura delle l equazioni di Kirchhoff avviene
adottando la procedura seguente:
•
si scelgono n – 1 nodi (tutti i nodi della rete meno uno) e si scrivono n – 1 equazioni
ai nodi, applicando a ogni nodo la legge di Kirchhoff delle correnti (KLC o primo
principio), con le modalità già descritte, scegliendo arbitrariamente i versi delle
correnti;
•
si scelgono l – n + 1 maglie e si scrivono l – n + 1 equazioni alle maglie, applicando
a ogni maglia la legge di Kirchhoff delle tensioni (KLV o secondo principio), con le
modalità già descritte, scegliendo arbitrariamente i versi di percorrenza e lasciando
come incognite le sole correnti;
•
si ottiene così un sistema lineare di n – 1 + l – n + 1 = l equazioni, risolvendo il
quale si ottengono i valori delle l correnti dei lati;
•
si valutano i segni dei risultati ottenuti, tenendo presente che il segno negativo indica
che il verso effettivo della corrente è opposto a quello inizialmente prefissato, il quale
va quindi cambiato se si vuole considerare positivo, da quel momento in poi, il valore
della corrente;
•
applicando le equazioni caratteristiche dei singoli bipoli si calcolano le tensioni, se
richieste

Esempio: Si calcolino le correnti circolanti nei lati della rete della sottostante figura e le
tensioni ai capi dei bipoli, considerando le serie E1-R1 ed E2-R2 come singoli bipoli attivi.
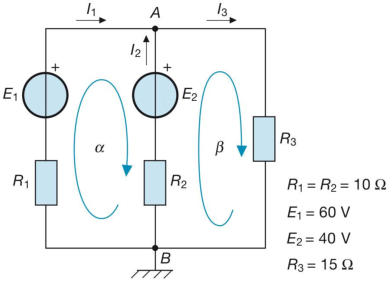
La rete è formata da l = 3 lati ed n = 2 nodi; occorre pertanto scrivere n – 1 = 1
equazione ai nodi e l – n + 1 = 2 equazioni alle maglie. Scegliendo il nodo A e le maglie
α e β, con i versi indicati nella figura B1.1, si ottengono le seguenti tre equazioni nelle
incognite I1, I2, I3 :
nodo
maglia
maglia
Ponendole a sistema e risolvendole con il metodo di sostituzione si ha


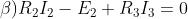



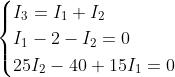



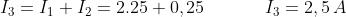

Tutte le correnti hanno segno positivo e, quindi, i versi scelti corrispondono a quelli
effettivi.
I due bipoli attivi, avendo correnti uscenti dal morsetto positivo della tensione, si
comportano come generatori reali di tensione, fornendo entrambi potenza al resistore R3.
I tre bipoli sono in parallelo, sottoposti alla stessa tensione VAB, per calcolare la quale si
può usare l’equazione caratteristica di uno qualsiasi dei bipoli. Calcolandola, per verifica,
in tutti e tre i modi si ottiene:
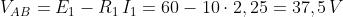
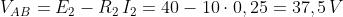
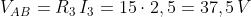

Presenza di generatori di corrente
Si supponga che nel lato di una rete vi sia un generatore ideale di corrente, che impone
la propria corrente impressa a tutti i bipoli del lato, collegati in serie tra loro. In questo
caso vi è una corrente incognita in meno, dal momento che la corrente impressa dal
generatore è un dato; però compare come incognita la tensione ai capi del generatore e,
quindi, nel complesso, il numero di incognite rimane invariato.
Il metodo più conveniente per risolvere casi del genere è quello sintetizzato nella
seguente regola:
in presenza di un numero p di lati contenenti generatori ideali di corrente con corrente
impressa nota, si considerano come incognite l – p correnti, riducendo di p il
numero delle equazioni alle maglie, con l’avvertenza di non scegliere come maglie
quelle che includono lati con generatori di corrente.
A tal riguardo si veda l’esempio seguente.

Del circuito di figura, calcolare le correnti nei lati e le tensioni ai capi dei generatori di
corrente

Nel caso in esame si ha: n = 4 nodi (A, B, C, D), l = 6 lati (A-B, A-C, A-D, B-C, B-D,
C-D), p = 2 lati con generatori ideali di corrente e quindi l–p = 4 equazioni, di cui n–1 = 3
ai nodi e una sola equazione alle maglie, a differenza delle tre necessarie nei casi ordinari.
Scegliendo i nodi A, B, C e la maglia α (maglia A-C-B-D-A che non contiene i due generatori
di corrente), con i versi indicati nella figura, si possono scrivere le seguenti equazioni:

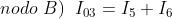


Sostituendo i valori noti, si ottiene il seguente sistema, nelle incognite I1, I2, I5 e I6;

risolvendo il quale (la soluzione viene omessa per brevità), si arriva ai seguenti valori:

I segni tutti positivi delle correnti indicano che i versi assunti sono quelli effettivi.
I valori delle tensioni ai capi dei generatori di corrente si calcolano usando il concetto di
tensione tra due punti, già precedentemente menzionato.
Scegliendo i percorsi B-D-A e C-B-D si ottiene:
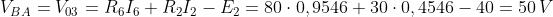
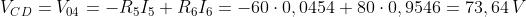
Bilancio delle potenze in una rete elettrica
In una rete elettrica sono presenti bipoli di vario tipo; precisamente:
•
utilizzatori passivi, costituiti da resistori che assorbono potenza elettrica, senza
generarne alcuna;
•
generatori ideali, di tensione e di corrente, che erogano agli altri bipoli della rete
tutta la potenza elettrica generata, in quanto hanno perdite nulle;
•
generatori reali, di tensione e di corrente, che erogano agli altri bipoli della rete la
differenza tra la potenza generata e quella persa al loro interno;
•
utilizzatori attivi che assorbono dalla rete una potenza pari alla somma della
potenza utilizzata e di quella persa al loro interno.
Poiché la rete è isolata rispetto all’esterno, è evidente che la somma delle potenze
erogate dai generatori (corrispondenti alle loro potenze utili) deve essere uguale alla
somma delle potenze assorbite dagli utilizzatori, attivi o passivi che siano.
Il bilancio delle potenze può quindi essere espresso con la seguente formula:

dove per utilizzatori passivi si intendono tutti i resistori della rete, eccetto quelli che
rappresentano le resistenze interne dei generatori reali e degli utilizzatori attivi reali


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





