



Ma a voi il calcio vi ha tarlato il cervello, ma fin da piccoli, eh?
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!


Massa
kilogrammo
kg
RISOLUZIONE DELLE RETI ELETTRICHE LINEARI

Scopo di questo capitolo,è ottenere i seguenti risultati :
•
conoscere i principali metodi di risoluzione di una rete
elettrica lineare;
•
saper risolvere completamente una rete, ricavandone
le grandezze elettriche di tutti i lati, mediante il metodo
di risoluzione indicato;
•
saper risolvere completamente una rete scegliendo
autonomamente il metodo di risoluzione più appropriato;
•
saper risolvere parzialmente una rete, calcolando le
grandezze elettriche richieste dalle specifiche del problema;
•
saper analizzare il comportamento dei bipoli costituenti
la rete e saper eseguire il bilancio energetico della stessa;
•
essere in grado di verificare sperimentalmente i metodi
di risoluzione studiati.
Tutti gli obiettivi si riferiscono a reti elettriche lineari di
media complessità, funzionanti in corrente continua e
alimentate da uno o più generatori
Risoluzione di un sistema di equazioni lineari

Sistema di equazioni lineari
Un’equazione nelle n incognite x1, x2, …, xn, si dice di 1° grado o lineare quando può
essere ridotta alla forma seguente, in cui tutte le incognite compaiono alla prima potenza:
dove a1, a2, …, an sono dei numeri reali noti, detti coefficienti delle incognite, e h è il
termine noto, anch’esso di tipo reale. L’equazione è omogenea se h = 0, non omogenea in
caso contrario.
Considerando un insieme di n equazioni nelle n incognite indicate, si ottiene un
sistema di equazioni lineari:

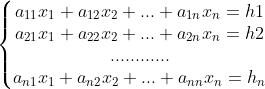
Si chiama soluzione del sistema un gruppo ordinato di n numeri che, sostituiti alle n
incognite, soddisfano tutte le equazioni del sistema.
Nel seguito, limitandosi a un massimo di tre equazioni, le incognite verranno indicate
con i simboli x, y e z.
Metodo di confronto
Il metodo di confronto è adatto ai sistemi di due equazioni e si applica usando la
seguente procedura:
1. si ricava dalle due equazioni la stessa incognita, ponendo ogni equazione
nella forma x = …, oppure y = …;
2. si uguagliano i secondi membri, ottenendo un’equazione in una sola incognita;
3. si risolve l’equazione, ricavando il valore dell’incognita;
4. si sostituisce il valore in una delle equazioni e si ricava l’altra incognita.
Per chiarire la procedura, si segua la risoluzione del seguente sistema:


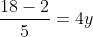



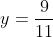
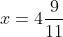

Metodo di sostituzione
Le operazioni da seguire per applicare il metodo di sostituzione sono le seguenti:
1. si ricava da un’equazione una delle incognite, ottenendo un’espressione in
funzione delle altre incognite;
2. si sostituisce l’espressione in tutte le restanti equazioni, ottenendo n – 1
equazioni in n – 1 incognite;
3. per questo sistema ridotto si ripetono le operazioni 1 e 2, fino a ottenere una
sola equazione in una incognita;
4. si risolve l’equazione e si ricava il valore dell’incognita;
5. rifacendo a ritroso il cammino percorso, si calcolano le altre incognite.
Per chiarire la procedura si segua la risoluzione del seguente sistema:
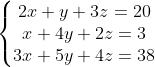
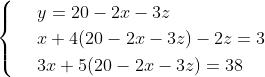
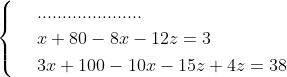

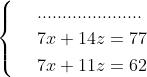



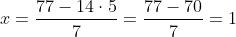

Metodo di riduzione
Nel caso di sistemi con due equazioni la procedura da seguire per applicare questo
metodo è la seguente:
•
si moltiplica ogni equazione per un numero reale diverso da zero, in modo
che i coefficienti di una incognita (per esempio x) risultino opposti nelle due
equazioni;
•
si sommano membro a membro le due equazioni, in modo da ottenere una
terza equazione, combinazione lineare delle due iniziali, in una sola incognita (y,
nell’esempio);
•
si risolve l’equazione ottenuta, determinando il valore di un’incognita;
•
si sostituisce tale valore in una delle equazioni iniziali e, risolvendola, si ottiene il
valore dell’altra incognita.
Per maggiori chiarimenti si consideri l’esempio seguente:

I coefficienti di x, 6 e 4, hanno minimo comune multiplo pari a 12, per cui,
moltiplicando la prima equazione per 2 e la seconda per – 3 e sommando membro a
membro, si ottiene:

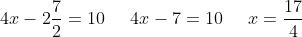
Metodo di Cramer
Quello di Cramer è un metodo applicabile a sistemi lineari con un qualsiasi numero
di equazioni e fa uso dei concetti di matrice e determinante.
Dato che tali concetti esulano dai limiti del testo, ci si limiterà a riportare le formule
risolutive valide per un sistema di due equazioni, scritto nella forma

La soluzione del sistema è data da

valida quando è verificata la condizione

Nel caso del sistema dell’esempio precedente, i coefficienti e i termini noti sono:
a1 = 6 b1 = −7 c1 = 1 a2 = 4 b2 = −2 c2 = 10
e, quindi, essendo rispettata la condizione:
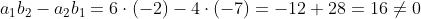
le soluzioni del sistema sono date da:
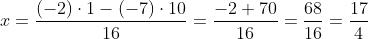
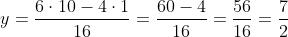


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





