



Con le mie ali riuscivo a volare fin sopra le nuvole.
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!


Massa
kilogrammo
kg
ATTIVITA’ DI LABORATORIO

L’attività di laboratorio è di fondamentale importanza nello
studio dell’Elettrotecnica e dell’Elettronica, sia come verifica
dei concetti studiati sia come approccio sperimentale ai vari
argomenti.
In questo capitolo vengono proposte delle esercitazioni
attinenti ai contenuti del modulo che richiedono l’impiego
della strumentazione di cui sono normalmente dotati i
laboratori elettrici, mentre per l’ultima proposta basta
l’uso di un semplice PC.
Misura della resistenza con il metodo
volt-amperometrico
Obiettivo dell’esercitazione è quello di misurare il valore
della resistenza elettrica di un resistore incognito, con l’uso
di un voltmetro e di un amperometro.
La prova comprenderà quindi la misura diretta della tensione, la misura diretta della
corrente e la misura indiretta della resistenza.
A seconda del valore presunto della resistenza incognita si potrà utilizzare uno degli schemi
riportati nella sottostante figura:

Lo svolgimento della prova è simile nei due casi. Avendo a disposizione un alimentatore
regolabile si possono eseguire più misure, con diversi valori di tensione e corrente,
tenendo conto dei valori di targa del resistore incognito Rx.
Per evitare un eccessivo riscaldamento del resistore è opportuno che la corrente massima
di prova non superi il valore In/10, dove In è la corrente nominale del resistore, e che la
misura venga effettuata per valori decrescenti della corrente.
Per ogni prova sugli strumenti verranno letti i valori della tensione misurata Vm e della
corrente misurata Im, dai quali si deduce il valore della resistenza misurata con la
relazione:

Se vengono utilizzati strumenti elettronici come i multimetri, che hanno valori della
resistenza interna tali da non influire in modo significativo sulla misura, oppure se non
sono noti i valori della resistenza interna del voltmetro e dell’amperometro, il valore
della resistenza incognita coincide con quello misurato: Rx = Rm.
Se, invece, sono noti i valori delle resistenze interne del voltmetro e dell’amperometro,
si calcola il valore della resistenza incongita con le relazioni:
• inserzione col voltmetro a valle:
• inserzione col voltmetro a monte:
Avendo effettuato più misure, il valore della resistenza incognita piò essere calcolato
come media aritmetica dei valori risultanti dalle varie prove.
Dai risultati delle misure è possibile ricavare la caratteristica volt-amperometrica del
bipolo incognito, riportando sul piano cartesiano V, I (o I, V) i punti corrispondenti ai
valori della tensione e della corrente misurati per ogni prova.
Se l’oggetto in prova è un normale resistore con comportamento lineare, i punti suddetti
devono stare su una retta passante per l’origine degli assi.

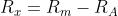
Misura della potenza con il metodo volt-amperometrico
Mediante il circuito di misura del paragrafo precedente può anche essere effettuata la
misura della potenza assorbita dal resistore in prova. In pratica, se il componente
usato non cambia, non è necessario fare altre misure ma si possono usare i valori della
tensione e della corrente della prova precedente.
La potenza misurata si calcola in modo indiretto con la relazione:
Se vengono utilizzati strumenti elettronici come i multimetri, che hanno valori della
resistenza interna tali da non influire in modo significativo sulla misura, oppure se non
sono noti i valori della resistenza interna del voltmetro e dell’amperometro, il valore
della potenza incognita coincide con quello misurato: Px= Pm.
Se, invece, sono noti i valori delle resistenze interne del voltmetro e dell’amperometro, si
calcola il valore della della potenza incognita con le relazioni:

• inserzione col voltmetro a valle:
• inserzione col voltmetro a monte:
Riportando su un grafico cartesiano i valori di Px sull’asse delle ordinate in funzione di
quelli di V sull’asse delle ascisse, per le varie misure effettuate, si ricava la curva della
potenza in funzione della tensione.
Se l’oggetto in prova è un normale resistore con comportamento lineare, avente
resistenza e conduttanza costanti al variare della tensione, i punti suddetti devono stare
sul ramo di una parabola avente come vertice l’origine degli assi, di equazione P = GV^2.
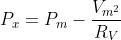

Generatore reale di tensione con carico variabile
Mediante l’uso di un PC e di un foglio elettronico (tipo Excel) si può studiare il
comportamento di un generatore reale di tensione, per il quale vengono assegnati i valori
della f.e.m. E e della resistenza interna Ri, collegato a un utilizzatore passivo di resistenza
Ru variabile da zero a RuM (da assegnare) con passo ΔRu, anch’esso da scegliere.
Per esempio, se si fissa Ri= 5 Ω e RuM = 25 Ω, si può scegliere ΔRu= 1 Ω e ottenere
una tabella di 25 valori oltre quello iniziale con Ru= 0, corrispondente alla condizione
di cortocircuito.
Per ogni valore della resistenza di carico si determinano i valori delle seguenti grandezze.
• corrente assorbita dal carico:
• tensione ai capi del carico:
• potenza generata:
• potenza utile:
• potenza persa:
Mediante le apposite funzioni del foglio elettronico si ricavano i grafici delle varie
grandezze, riportando sull’asse delle ascisse i valori di Ru, da zero a RuM. In accordo
con la teoria del bipolo generatore, i grafici cartesiani dovranno rispettare i seguenti
andamenti:
• la corrente dovrà diminuire all’aumentare di Ru, partendo dal valore Icc= E/Ri che
si ha con resistenza di carico nulla;
•
la tensione dovrà aumentare al crescere di Ru, partendo dal valore V = 0 in
cortocircuito;risulta, infatti, che se la corrente diminuisce si riduce anche la
c.d.t. interna al generatore e la tensione sul carico aumenta;
•
la potenza generata dovrà diminuire all’aumentare di Ru, dato che diminuisce l’intensità
di corrente alla quale è proporzionale
•
la potenza utile dovrà aumentare con Ru fino a un valore massimo che si avrà per
Ru= Ri (condizione di adattamento) e poi diminuirà al crescere ulteriore di Ru; il valore
iniziale sarà Pu= 0 per V = 0 (cortocircuito), mentre il valore massimo sarà pari a
PuM = E2/(4 Ri);
•
la potenza persa dovrà diminuire all’aumentare di Ru, essendo legata al quadrato
dell’intensità di corrente che, a sua volta, diminuisce
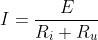

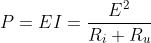




Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





