



Chi tutto dona, tutto abbandona.
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!


Massa
kilogrammo
kg
GENERATORI

Circuito equivalente del generatore reale
Nelle pagine precedenti, sono stati introdotti due bipoli ideali
chiamati, rispettivamente, generatore ideale di tensione e
generatore ideale di corrente.
Si supponga ora di voler ricavare un bipolo che rappresenti un
generatore elettrico reale; occorre tenere presenti i seguenti
aspetti:
•
un generatore elettrico non è mai solo “di tensione” o solo
“di corrente”; esso, in realtà,fornisce al circuito esterno
una potenza elettrica, che esiste solo se vi sono contempo-
-raneamente tensione e corrente; parlare di generatore di
tensione o di corrente serve solo a indicare qual è la gran-
-dezza elettrica che viene maggiormente messa in risalto;
•
all’interno di un generatore reale vi sono dei fenomeni dissipativi dovuti a cause elettriche,
magnetiche e meccaniche e quindi una parte della potenza generata viene perduta
all’interno del componente; per tener conto di tale perdita bisogna inserire una resistenza
interna nel circuito equivalente.
Per rappresentare con un circuito equivalente un generatore elettrico reale, funzionante in
corrente continua, vengono comunemente usati due modelli, corrispondenti a due bipoli reali,
detti rispettivamente:
•
generatore reale di tensione (figura a), formato dalla serie tra un generatore
ideale di tensione e un resistore; esso può anche essere visto come il circuito
equivalente serie del generatore;
•
generatore reale di corrente (figura b), formato dal parallelo tra un generatore
ideale di corrente e un resistore; può anche essere visto come il circuito equivalente
parallelo del generatore

In entrambi i casi la resistenza Ri ha il significato di resistenza interna del generatore e,
insieme alla f.e.m. E o alla corrente impressa Io, dipende dalla costituzione interna
dell’apparecchio.
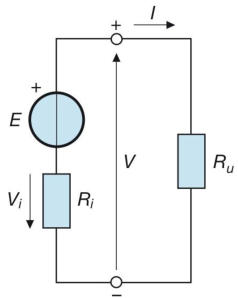
Generatore reale di tensione
Si consideri la sottostante figura un generatore reale di tensione, collegato a una
resistenza Ru che rappresenta la resistenza equivalente dell’utilizzatore connesso al
generatore (resistenza di carico).
Sotto l’azione della f.e.m. nel circuito circolerà una corrente I
che determinerà una caduta di tensione interna Vi nel genera-
-tore. La tensione V indica invece la d.d.p. tra i due morsetti del
generatore e corrisponde alla tensione applicata sulla resistenza
di carico.
Applicando la legge di Kirchhoff delle tensioni all’unica maglia
presente, si ottiene:
e quindi:
Questa espressione dice che in una determinata condizione di
carico la tensione V fornita dal generatore è minore della
f.e.m. E; tale differenza corrisponde alla c.d.t. interna e
dipende in maniera direttamente proporzionale dalla corrente
erogata e dalla resistenza interna.


La soprastante ultima equazione rappresenta anche, in forma analitica, la caratteristica
esterna del bipolo, ossia la legge V = f(I), considerando costanti i parametri E ed Ri e
utilizzando la convenzione di segno dei generatori.
La medesima equazione è quella di una retta: scrivendola infatti nella forma
V = − RiI + E e confrontandola con l’equazione caratteristica della retta y = mx + q, si
deduce che (− Ri) rappresenta il coefficiente angolare ed E l’intercetta sull’asse delle
ordinate.
Il tracciamento della caratteristica esterna in forma grafica si può fare considerando due
condizioni tipiche di funzionamento del generatore, corrispondenti ai due punti di interse-
-zione della retta con gli assi cartesiani.
Funzionamento a vuoto
Si ha quando il generatore non eroga corrente, ossia quando il carico non è collegato (la
resistenza di carico può essere considerata infinita), come indicato nella sottostante figura:

Ponendo I = 0 si ha che la c.d.t. interna è nulla e la tensione a vuoto del generatore assume
il valore:

Il punto (0, Vo) della caratteristica esterna indica tale funzionamento.
Funzionamento in cortocircuito
Si ha quando il generatore non fornisce tensione ai morsetti essendo collegato a un
cortocircuito ideale (la resistenza di carico può essere considerata nulla), come
indicato nella figura (b).
Ponendo V = 0 , si ha che la tensione interna sviluppata dal generatore (f.e.m. E) coincide
con la c.d.t. interna e la corrente erogata assume il valore della corrente di cortocircuito,
che si ricava da:
Il punto (Icc, 0) della caratteristica esterna indica tale funzionamento.

Caratteristica esterna
Tracciando la retta passante per i due punti precedentemente determinati, si ottiene
la caratteristica esterna del bipolo in forma grafica, riportata nella sottostante figura:
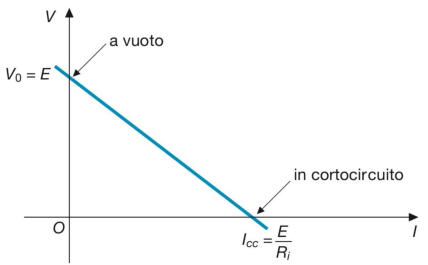
Caratteristica
volt-amperometrica
del generatore
reale di tensione.
L’esame della figura A2.46 consente di classificare il bipolo in esame come bipolo
attivo lineare, essendo la caratteristica una retta non passante per l’origine.
Punto di lavoro
La determinazione del punto di lavoro del generatore richiede il calcolo della tensione V e
della corrente I corrispondenti a un dato valore della resistenza di carico Ru.
Per la sua determinazione analitica si applica la legge di Ohm al carico, ottenendo:
Confrontando l’espressione precedente con le precedenti si ha:
da cui si ottiene il valore della corrente erogata dal generatore in funzione dei suoi
parametri interni E ed Ri e della resistenza di carico Ru :
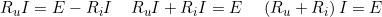
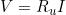
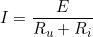
Il valore della tensione V si calcola con le formule già citate.
La determinazione del punto di lavoro può anche essere fatta graficamente,
intersecando la caratteristica del generatore con quella del carico, che è una retta
passante per l’origine, disegnata con la convenzione di segno degli utilizzatori (figura a).
Dato che i due bipoli devono avere la stessa tensione e la stessa corrente, il punto di lavoro
non può essere che quello d’intersezione P.
È importante notare che, a parità di altre condizioni, la diminuzione della resistenza Ru,
facendo abbassare la caratteristica del carico, determina lo spostamento del punto di lavoro
del generatore, con l’aumento della corrente e la diminuzione della tensione, come mostrato
nella figura (b).
Per Ru variabile da infinito a zero il punto P si sposta da quello a vuoto a quello di corto-
-circuito

(a)
(b)
Potenze e rendimento
Si consideri l’espressione e la si scriva nella forma:
Moltiplicandone tutti i termini per la corrente si ottiene:
Dove tutti i termini sono delle potenze elettriche, a cui si possono attribuire dei precisi
significati.
Il termine:
rappresenta la potenza generata dal bipolo, dipendente dalla sua tensione interna E;
essa è la potenza elettrica che il generatore produce tramite la trasformazione della
potenza di altro tipo (meccanica, chimica ecc.) che gli viene fornita.
Il termine
è invece la potenza utile del generatore, ossia quella che effettivamente esso fornisce al
circuito esterno, dipendente dalla tensione V con cui il generatore alimenta il carico ai suoi
morsetti.
Applicando la legge di Ohm al resistore Ru si ha anche:
mentre il termine:
rappresenta, infine, la potenza persa all’interno del generatore, conglobata nella potenza
dissipata per effetto Joule dalla resistenza interna Ri. Tale potenza è anche data da:
La può pertanto essere espressa nella seguente forma:
e definisce il bilancio delle potenze del generatore reale: la potenza che viene
complessivamente generata è somma della potenza effettivamente fornita al carico
esterno (utile) e di quella persa all’interno del generatore.
Da ques’ultima relazione si ricavano le formule equivalenti:



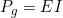
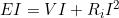



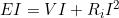


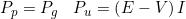
Si definisce rendimento del generatore il rapporto tra la potenza utile e quella generata:
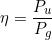
Altre formule derivate per il calcolo del rendimento sono le seguenti:
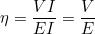
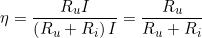
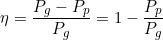
Il valore del rendimento, essendo un rapporto tra grandezze omogenee, è un numero
adimensionato; esso può variare tra 0 e 1, dove si ha:
•
η = 0 quando Pu= 0, ossia quando Ru= 0 (funzionamento in cortocircuito);
•
η = 1 quando Pu= Pg, ossia quando Pp= 0 e quindi Ri= 0 (generatore ideale senza
resistenza interna).
Nel caso del funzionamento a vuoto, non essendoci corrente, tutte le potenze sononulle e
non ha senso parlare di rendimento.
Spesso il valore del rendimento si esprime percentualmente, moltiplicando per cento il suo
valore decimale; le espressioni del rendimento percentuale si ottengono facilmente da
quelle viste in precedenza:



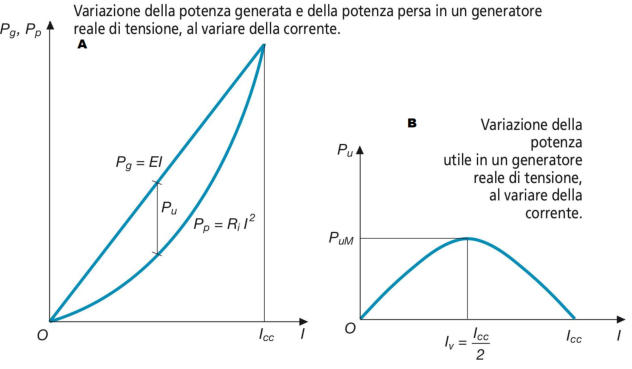
Analisi delle potenze al variare del carico esterno
La condizione di carico del generatore può variare tra i seguenti limiti:
•
funzionamento a vuoto, con Ru ∞, V = V0= E, I = 0
•
funzionamento in cortocircuito, con Ru= 0, V = 0, I = Icc= E/Ri
Per rappresentare le potenze in funzione della corrente erogata dal generatore si consideri
che:
•
la potenza generata Pg= EI, con E costante, è analoga all’espressione y = mx, che è
l’equazione di una retta passante per l’origine; la potenza generata è nulla a vuoto
ed è massima in cortocircuito
•
la potenza persa Pp= RiI^2, con Ri costante, è analoga all’espressione y = ax^2,
che è l’equazione di una parabola con concavità verso l’alto (a > 0), asse coincidente
con quello delle ordinate e con vertice nell’origine; la potenza persa è nulla a vuoto
e massima in cortocircuito, quando coincide con quella generata;
•
la potenza utile Pu= Pg− Pp è data dalla differenza tra le ordinate delle due curve
precedenti; si ha anche Pu = − RiI^2 + EI, analoga all’espressione y = ax^2 + bx,
che rappresenta una parabola con concavità verso il basso (a < 0) e passante per
l’origine (c = 0); la potenza utile è nulla sia a vuoto che in cortocircuito.
Rappresentando le tre curve in funzione della corrente si ottengono i grafici delle
figure a) e b)
Il regime di funzionamento a cui corrisponde il massimo valore di potenza utile corrisponde
alla condizione di adattamento del generatore. Tale condizione di carico si ha in corrispo-
-ndenza del vertice della parabola, ossia per una corrente pari a:
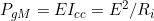


come si può facilmente verificare analiticamente mediante le espressioni delle coordinate
del vertice.
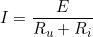
Confrontando quest’espressione con si vede che tale regime di funzionamento
si ha quando la resistenza di carico è tale da soddifare la relazione:

Nei circuiti elettronici la condizione di adattamento è molto importante: un generatore è
adattato quando è caricato con un circuito esterno di resistenza equivalente a quella
interna del generatore: in tale condizione esso eroga la potenza utile massima.
Nella condizione di adattamento si ha:

e, quindi, la massima potenza utile del generatore sarà pari a
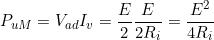
Il rendimento nella condizione di adattamento è dato da:

La condizione di massima potenza utile non è conveniente per i generatori di grande
potenza, dato che, con rendimento 0,5, la potenza utile è solo il 50% di quella generata
e l’altro 50% se ne va in perdite.
Nei circuiti elettronici, invece, le potenze in gioco sono modeste e tale condizione di
funzionamento non comporta, in assoluto, fenomeni dissipativi gravi

Un esempio: Un generatore reale di tensione, avente E = 100 V ed Ri= 5 Ω, è collegato a
un carico di resistenza Ru= 20 Ω. Calcolarne il punto di lavoro (corrente e tensione), le
potenze (generata,utile, persa) e il rendimento.
La risoluzione del problema è immediata; applicando le formule già viste, si ottengono i
valori delle grandezze richieste:

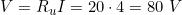



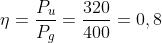

Un ulteriore esempio :Un generatore reale di tensione, avente E = 10 V ed Ri= 2,5 Ω, eroga
al carico a cui è collegato una potenza pari a 8 W.
Calcolarne il punto di lavoro, la resistenza del carico, la potenza generata, quella persa,
il rendimento.
Determinare il valore della resistenza da collegare in serie o in parallelo a quella di carico per
ottenere la condizione di adattamento del generatore.
Dall’esame della sottostante figura si vede che per ogni valore della potenza utile vi sono
due diversi valori della corrente, entrambi possibili, escluso il punto di vertice della parabola,
a cui corrisponde la potenza utile massima e un solo valore di corrente.
Nel caso in esame tale potenza è pari a:


La potenza utile erogata al carico (8 W) è inferiore a tale valore e
quindi vi saranno due possibili valori della corrente, corrispondenti
a due diversi punti di lavoro.
Per il loro calcolo si parte dalla relazione che lega le potenze, ottenendo:
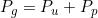
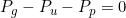


Cambiando segno e ordinando i vari termini, si arriva alla seguente equazione di secondo
grado:

risolvendo la quale si ricavano i due valori della corrente:
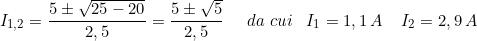
Il calcolo delle altre grandezze incognite dovrà essere fatto separatamente per le due
soluzioni.
Prima soluzione
Applicando le formule già viste si ottiene:
Essendo Ru> Ri, per ottenere l’adattamento del generatore occorre ridurre la resistenza
complessiva del carico.
Questo si può ottenere ponendo in parallelo a Ru una resistenza R, tale che sia soddisfatta
la relazione:
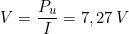




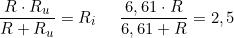
risolvndo la quale:

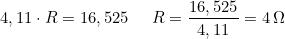
Seconda soluzione
Procedendo allo stesso modo si ha:


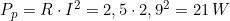

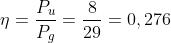
Si può notare che nel secondo caso il rendimento è piuttosto basso e la maggior parte della
potenza generata viene persa nel generatore.
In questa condizione di funzionamento si ha Ru< Ri e quindi, per ottenere la condizione di
adattamento, bisogna aumentare la resistenza complessiva del carico, ponendo in serie
ad Ru una resistenza R di valore tale che sia:
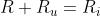



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





