



La fantasia è il potere più grande della mente
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!


Massa
kilogrammo
kg
BIPOLI IN PARALLELO

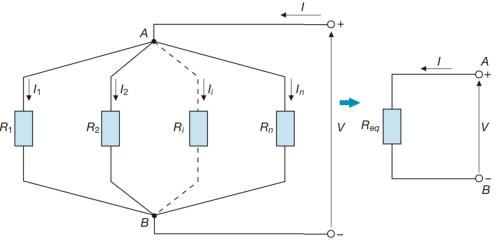
Collegamento in parallelo dei resistori
Si considerino n resistori collegati in parallelo tra i nodi A e B
e quindi soggetti tutti alla stessa tensione V, supposta positiva
sul morsetto A.
Nei singoli resistori, da A verso B, circoleranno delle correnti,
la cui somma, per il primo principio di Kirchhoff, sarà pari alla
corrente totale I
Anche in questo caso il problema consiste nel determinare la resistenza del resistore
equivalente, che sarà pertanto interessato dalla corrente totale e dalla tensione V comune a
tutti i resistori.
Utilizzando le conduttanze dei vari resistori si ottiene la corrente totale


Applicando la stessa legge al resistore equivalente, di conduttanza Geq, si ottiene

Il confronto tra le soprastanti relazioni, consente di esprimere la conduttanza equivalente
da cui la regola:
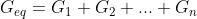
la conduttanza equivalente di n resistori in parallelo è data dalla somma delle
conduttanze dei singoli resistori.
Indicando con Gi la conduttanza del termine i-esimo del parallelo, si ha anche:
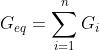
Nel caso particolare di n resistori aventi uguale conduttanza G, la conduttanza
equivalente risulta pari a n volte la conduttanza di un singolo resistore:
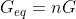
Nota: la conduttanza equivalente, è immediato il calcolo della resistenza equivalente,
utilizzando l’espressione generale:

Volendo comunque esprimere la resistenza equivalente in funzione delle singole resistenze,
si può esplicitare la formula precedente, ottenendo:
oppure
nel caso di n resistori uguali, si ottiene
da cui :
Questa espressione mostra che
la resistenza equivalente di n resistori uguali in parallelo è pari alla resistenza di
un singolo resistore diviso il numero di rami del parallelo.
Particolarmente importante è il caso di due resistori in parallelo, di resistenze R1 e R2
Dalle soprastanti espressioni si ricava:
da cui:
Le potenze assorbite dai singoli resistori del parallelo :
….
La potenza totale assorbita dal circuito parallelo sarè uguale a:
da cui
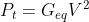



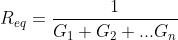

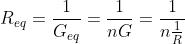

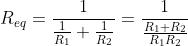


L’espressione porta alla conclusione che la potenza totale assorbita da un gruppo di resistori
in parallelo è, a parità di tensione, uguale a quella del resistore equivalente.
La regola enunciata, verificata sia per il collegamento in serie che per quello in
parallelo, ha validità generale e si può così esprimere:
la potenza totale di un gruppo di resistori, pari alla somma delle singole potenze,
è uguale a quella del resistore equivalente, qualunque sia il collegamento dei
resistori.

Ad esempio, si calcoli la resistenza equivalente di tre resistori in parallelo, aventi resistenze
pari a 1,2 kΩ, 1,8 kΩ, 3,6 kΩ; supponendo di applicare al parallelo la tensione V = 48 V,
si calcolino le potenze assorbite dai singoli resistori e quella totale.
Le conduttanze dei vari resistori sono uguali a:
per cui
ne risulta che:
Allo stesso risultato si arriva operando con le resistenze:





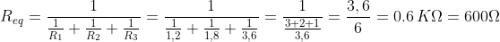
Le potenze assorbite dai singoli resistori sono date da:
e quindi la potenza totale è data da
allo stesso risultato si arriva anche

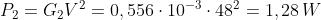




Adesso prendiamo in esame quattro resistori uguali, connessi in parallelo e alimentati con
tensione 20 V, che assorbono una potenza totale di 16 W.
Si calcoli il valore della resistenza di ogni resistore.
Applicando le formule inverse ricavabili da quelle finora mostrate, si ottiene:


e, quindi, la resistenza di ogni resistore è data da:
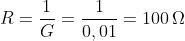

Regola del partitore di corrente
Questa espressione consente di calcolare la corrente in un ramo del parallelo in funzione
della corrente totale e costituisce la regola del partitore di corrente, così esprimibile:
la corrente in un qualsiasi resistore di un gruppo di resistori connessi in parallelo è pari alla
corrente totale moltiplicata per un coefficiente di riduzione, dato dal rapporto tra la condut-
-tanza del resistore considerato e quella equivalente del parallelo.
Si può notare che la corrente è proporzionale alla conduttanza e quindi, per il
collegamento in parallelo, vale la regola che:
il resistore di conduttanza maggiore (ossia di resistenza minore) è interessato dalla
corrente maggiore e viceversa.
Nel caso di due soli resistori in parallelo (arco doppio) è possibile ricavare due formule
operative molto usate in pratica, utilizzando una espressione già vista. Con semplici
passaggi si ottiene:
ed infine
e per l’altro resistore

Si riconsideri il parallelo della figura a
lato, con l’intento di calcolare la corrente
che interessa un generico resistore.
Applicando la legge di Ohm al termine
i-esimo del parallelo, si ha:
Ricavando la tensione e sostituendo :



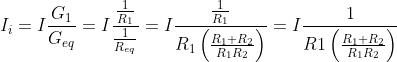
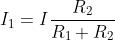
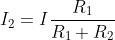
L’esame delle soprastanti espressioni, consente di formulare la seguente regola:
la corrente in uno dei due rami di un arco doppio è data dalla corrente totale per il
rapporto di riduzione tra la resistenza dell’altro ramo e la somma delle due resistenze.
Nel caso di n resistenze uguali di valore R, l’espressione del partitore diventa:
da cui



e, quindi, la corrente totale si ripartisce in n parti uguali

Ad esempio, dal precedente esempio, si calcolino le correnti di tre resistori in parallelo,
aventi resistenze pari a 1,2 kΩ, 1,8 kΩ, 3,6 kΩ; supponendo di applicare al parallelo la
tensione V = 48 V.
Dall’esempio precedente, abbiamo calcolato che:
quindi la corrente totale è data da:


Applicando la regola del partitore di corrente si ha:
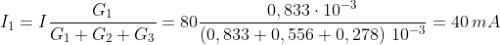
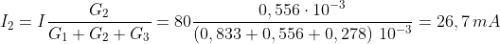



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





