



Una fede che non sia pensata è niente
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!



Massa
kilogrammo
kg
BIPOLI IN SERIE


Si consideri ancora il circuito visto in precedeza, il collegame-
-nto tra il generatore ideale di corrente I01 e il resistore R1.
Esso è tale che la corrente impressa dal generatore interessa
anche il resistore, non essendoci bipoli intermedi in grado di
derivare una parte della corrente.
Tale collegamento è detto in serie; in generale si ha che
due o più bipoli sono collegati in serie quando sono soggetti
alla stessa corrente.

Il collegamento in serie è caratterizzato dall’assenza di nodi tra i vari bipoli, dato che nei
punti intermedi (punto A ) confluiscono sempre due soli bipoli.
Nella figura a sinistra è rappresentata una serie di n
bipoli, tutti caratterizzati dalla stessa corrente I ma da
tensioni diverse V1, V2,…,Vn e facenti capo ai punti
A e B.
Nei riguardi della rete a cui sono collegati il complesso
è equivalente a un unico bipolo, avente come corrente
il valore I e come tensione totale la tensione VAB,
calcolata col metodo della tensione tra due punti.
Si parla in questo caso di equivalenza esterna, nel
senso che è possibile sostituire a una serie di bipoli
un bipolo equivalente avente la stessa tensione e la
stessa corrente, senza modificare il comportamento
del circuito esterno.
L’equivalenza non vale ai fini interni: è evidente,
infatti, che nel bipolo equivalente non figurano più le
tensioni dei singoli bipoli componenti
Serie di n bipoli
e bipolo equivalente.
Si consideri ora, sempre per il circuito da cui siamo partiti, il collegamento tra il generatore
ideale di tensione E1 e il resistore R2.
I due bipoli sono connessi in modo tale che la tensione impressa dal generatore agisce anche
sul resistore, ossia sono sottoposti alla stessa tensione.
Tale collegamento è detto in parallelo o in derivazione; in generale si ha che due o più bipoli
sono collegati in parallelo quando sono soggetti alla stessa tensione.
Il collegamento in parallelo è caratterizzato dal fatto che i bipoli sono collegati agli stessi
nodi della rete.
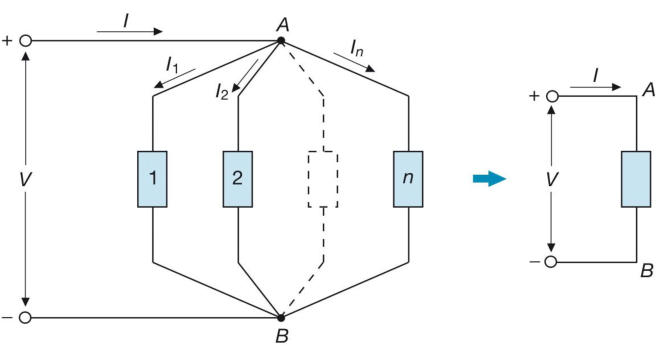
Parallelo di n bipoli
e bipolo equivalente
Nella soprastante figura è rappresentato un parallelo di n bipoli, tutti caratterizzati dalla
stessa tensione V ma da correnti diverse I1, I2,…, In e collegati ai nodi A e B.
Anche in questo caso è possibile sostituire il complesso di n bipoli con un unico bipolo
equivalente,
caratterizzato dalla stessa tensione V e dalla corrente totale I, somma
algebrica della corrente dei singoli bipoli.
Si definiscono reti di tipo serie-parallelo quelle reti costituite da bipoli tutti collegati in
serie o in parallelo; in questi casi si può arrivare al bipolo equivalente mediante
successive riduzioni di bipoli in serie o in parallelo.
Non tutte le reti sono di tipo serie-parallelo: un esempio è
la rete a ponte della figura a sinistra.

Rete a ponte
In questo caso non è possibile individuare una successione
di operazioni di riduzione di tipo serie-parallelo che consenta
di arrivare al bipolo equivalente.
Nel caso che i bipoli siano tutti resistori, il bipolo equivalente
si può determinare con le trasformazioni stella-triangolo chr
vedremo in seguito.

Collegamento in serie dei resistori
Si considerino, come nella figura sottostante, n resistori collegati in serie e quindi interessati
dalla stessa corrente I, circolante dal morsetto A al morsetto B in seguito all’applicazione
della tensione V ai capi della serie.
Il problema è quello di determinare la resistenza del resistore
equivalente alla serie, ossia di quel resistore che, sottoposto alla
stessa tensione, assorbe il medesimo valore di corrente;
l’inserzione del resistore equivalente al posto della serie
originaria non comporta variazioni per la rete esterna di
alimentazione.
Tenendo conto che le tensioni sui singoli resistori hanno tutte
la polarità positiva nel punto di ingresso della corrente, la
tensione totale tra i punti A e B si calcola semplicemente come
somma delle tensioni dei singoli resistori.

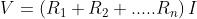
Applicando la legge di Ohm al resistore equivalente, si ottiene:


Il confronto tra le succitate espressioni consente di trovare immediatamente la formula per
il calcolo della resistenza equivalente di una serie di n resistori:
da qui la regola:
la resistenza equivalente di n resistori in serie è data dalla somma delle resistenze
dei singoli resistori.
L’espressione di resistnza equivalente, può anche essere scritta in forma contratta,
indicando con Ri la resistenza del generico termine i-esimo della serie e introducendo il
concetto di sommatoria:

Nel caso particolare di n resistori aventi uguale resistenza R, la resistenza equivalente
risulta pari a n volte la resistenza di un singolo resistore:

Tenendo conto che, per effetto Joule, ogni resistore assorbe dal circuito esterno una
potenza elettrica data dall’espressione
, le potenze assorbite dai singoli
resistori della serie sono pari a
La potenza totale assorbita dalla serie risulta:


ovvero:

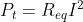
La soprastante espressione porta alla conclusione, a cui si poteva arrivare anche
intuitivamente, che
la potenza totale assorbita da un gruppo di resistori in serie è, a parità di corrente,
uguale a quella assorbita dal resistore equivalente

Ad esempio, calcoliamo la resistenza equivalente di una serie di tre resistori aventi
resistenze pari a 100 Ω, 180 Ω, 220 Ω. Calcoliamo le potenze assorbite dai singoli resistori
e quella totale, supponendo di applicare alla serie una tensione totale di 15 V.
La resistenza equivalente è data da:
la corrente che interessa tutta la serie è pari a:
Le potenze dei singoli resistori sono date da:





La potenza totale può essere calcolata nei due seguenti modi, ottenendo il
medesimo risultato:



Sempre per esempio, una serie di quattro resistori uguali, alimentata con tensione 12 V,
assorbe la potenza di 2 W.
Calcoliamo il valore della resistenza di ogni resistore.


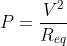
Per risolvere il quesito è opportuno cercare un legame tra la potenza totale e la tensione.
Dalla legge di Ohm si ottiene :
La cui formula inversa, consente di ricavare la resistenza equivalente
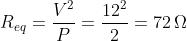
Trattandosi di quattro resistenze uguali, la resistenza di ogni resistore è ¼ di quella
totale:


Regola del partitore di tensione
Si riconsideri la serie esposta all’inizio, con lo scopo di calcolare la tensione ai capi di
un qualsiasi resistore.
Applicando la legge di Ohm a un generico resistore della serie (termine i-esimo), si
ha:
Ricavando la corrente, si ha
da cui
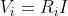


Quest’ultima espressione consente di calcolare la tensione ai capi di un resistore della
serie in funzione della tensione totale e costituisce la regola del partitore di tensione,
così esprimibile:
la tensione su un qualsiasi resistore di un gruppo di resistori connessi in serie è pari
alla tensione totale moltiplicata per un coefficiente di riduzione, dato dal rapporto
tra la resistenza del resistore considerato e quella equivalente della serie.
È possibile notare che la tensione è proporzionale alla resistenza e quindi per il
collegamento in serie vale la regola che:
il resistore di resistenza maggiore è soggetto alla tensione maggiore e viceversa,
ossia la tensione si ripartisce in maniera direttamente proporzionale alle resistenze
dei vari elementi della serie.
Nel caso di n resistenze uguali di valore R, la soprastante espressione diventa:
da cui:
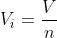

e, quindi, la tensione totale si ripartisce in n parti uguali


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





