



Non troverai mai la felicità finché non smetterai di cercarla
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!




Massa
kilogrammo
kg
VARIAZIONI DELLA RESISTENZA E DELLA RESISTIVITA’ CON LA TEMPERATURA
Vari fattori influiscono sul valore della resistenza elettrica,
modificando i parametri da cui essa dipende (resistività, lun-
-ghezza, sezione).
Una delle grandezze fisiche che maggiormente incide sul
valore della resistenza è la temperatura: per la maggior parte
dei materiali metallici la conducibilità elettrica diminuisce
all’aumentare della temperatura e quindi la resistività aumenta.
Fisicamente il fenomeno si può spiegare considerando che nei
solidi cristallini gli atomi vibrano attorno alla loro posizione di
equilibrio e queste vibrazioni interferiscono con il movimento
degli elettroni di conduzione, determinando quel complesso di
azioni contrastanti la conduzione delle cariche che viene
espressa analiticamente con il concetto di resistività elettrica
e che determina, in ultima analisi, una perdita di energia degli
elettroni, perdita che deve essere compensata dal generatore
esterno, per mantenere la conduzione nel circuito.
Aumentando la temperatura, l’agitazione termica aumenta e cresce pertanto anche l’opposi-
-zione del mezzo conduttore al passaggio della corrente. Alla temperatura dello zero assoluto,
cessando del tutto l’agitazione termica degli atomi, la resistività dovrebbe essere nulla; in
realtà subentrano altri fattori di disturbo, come i difetti reticolari e la presenza di impurità,
che producono una resistività residua . L’andamento della resistività in funzione della
temperatura assume pertanto la forma del grafico di figura 13, nel quale la resistività alle


[13]
Variazione della resistività nei metalli.
temperature di normale funzionamento risulta pro-
-porzionale alla temperatura, con una legge lineare.
L’espressione R = ρl/S mostra che la resistenza
dipende dalla resistività del materiale, dalla lunghezza
e dalla sezione del conduttore; si riterrà trascurabile la
variazione di resistenza dovuta alla variazione di
lunghezza e sezione per cause termiche, considerando
come unico fattore influente la resistività.
In questo modo, ai fini pratici, non cambia nulla se si
considera la variazione della resistività o della resiste-
-nza, essendo le due grandezze legate da un fattore
costante.
Per una trattazione analitica del fenomeno, si indichi con R0 il valore della resistenza alla
temperatura di 0 °C (273 K) e con R quello alla temperatura generica
; la differenza tra i
due valori rappresenta la variazione di resistenza:
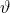

Per semplificare lo sviluppo analitico si può ritenere tale differenza direttamente
proporzionale alla variazione di temperatura , alla resistenza iniziale R0
e ad un coefficiente
dipendente dal tipo di materiale; esprimendo queste considerazioni
in forma matematica si ha:

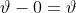
[16]

e sostituendo nell’espressione precedente, si ottiene :

e quindi:

[17]
La soprastante relazione consente di calcolare il valore della resistenza a una certa
temperatura, in funzione del suo valore alla temperatura di riferimento, del salto termico e
del fattore
, detto coefficiente di temperatura della resistenza, dipendente dal tipo
di materiale.
Ricavando la formula inversa della [16] si ottiene:

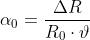
[18]
che consente di dedurre il significato del coefficiente di temperatura. Infatti, se nella [18]
si pone , i valori di
coincidono e, quindi, il valore
del coefficiente di temperatura rappresenta la variazione di resistenza di un conduttore
con resistenza iniziale 1 Ω, dovuta alla variazione di temperatura di 1 K (o di 1 °C).
La sua unità di misura si ricava dalla [18]:

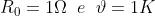
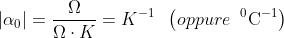
Dalla [17], in base alle ipotesi fatte inizialmente, è possibile ricavare un’analoga
relazione per la resistività:
da cui :
[19]
da cui si deduce che
è anche il coefficiente di temperatura della resistività


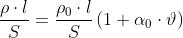

Andamento della resistenza
in funzione della temperatura,
ipotizzando α0 costante.
Supponendo che il valore di resti costante al variare della temperatura, le espressioni
[17] e [19] indicano una variazione lineare della resistenza (o della resistività), corrispo-
-ndente all’andamento del soprastante grafico, valido nel caso che la resistenza aumenti
con la temperatura.
Spesso la temperatura di riferimento si assume pari a 20 °C; in questo caso bisogna
considerare come salto termico la differenza e l’espressione [17] diventa:
[20]
dove è il valore della resistenza iniziale, R quello alla temperatura considerata
e è il valore del coefficiente alla temperatura di 20 °C.
Un’espressione analoga vale per la resistività.
Nella sottostante tabella sono riportati i valori della resistività, della conduttività e del
coefficiente di temperatura di alcuni materiali di uso comune nelle applicazioni elettriche.



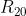

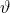
Caratteristiche elettriche di alcuni materiali conduttori


Materiale
Resistività a 20°C
(Ω mm2 /m )
Conduttività a 20°C
(MS/m)
Coefficiente di temper-
atura a 20°C(K–1)
Argento
0,0163
61,3
3,8 × 10–3
Rame crudo
0,0178
56,2
3,81 × 10–3
Rame ricotto
0,0175
57,1
3,93 × 10–3
Rame ricotto campione
0,017241
58,0
3,9 × 10–3
Alluminio
0,0284
35,2
4 × 10–3
Aldrey
0,032
31,2
3,6× 10–3
Tungsteno
0,055
18,2
4,5× 10–3
Ferro puro
0,098
10,2
6× 10–3
Acciaio
0,10-0,25
10 - 4
4,7× 10–3
Ferro silicio (Si= 1-5%)
0,27-0,67
3,7 - 1,5
/
Argentana
0,38
2,63
0,07× 10–3
Manganina
0,44
2,27
0,015× 10–3
Costantana
0,5
2,0
0,02× 10–3
Carbone
66,7
0,015
-0,45× 10–3
Zinco
0,06
16,7
3,7× 10–3
Stagno
0,12
8,33
4,3× 10–3

Riguardo alla variazione della resistenza con la temperatura si possono fare, prendendo in
esame la relazione [16], le seguenti considerazioni:
•
essendo entrambi positivi,
hanno lo stesso segno;
•
se è positivo lo è anche ΔR e, quindi, la resistenza aumenta con la temperatura,
come avviene, anche se in misura minima, in molti materiali conduttori (rame,
alluminio, argento ecc.) e in modo accentuato per i materiali usati nella costruzione
dei termistori PTC (Positive Temperature Coefficient);
•
se è negativo lo è anche ΔR e, quindi, la resistenza diminuisce con la temperatura,
come avviene in modo significativo in alcuni ossidi metallici usati per la costruzione
dei termistori NTC (Negative Temperature Coefficient)




•
nel caso fosse verificata la condizione
= 0 si avrebbe ΔR = 0, ossia la resistenza
non varierebbe con la temperatura (caso ideale); in realtà vi sono dei materiali che si
avvicinano molto a questa condizione e vengono usati per costruire resistori
campione da laboratorio, per i quali la variazione della resistenza comporterebbe un
errore di misura.
Un altro modo per valutare la variazione di resistenza con la temperatura si basa sul confro-
-nto tra i valori della resistenza a due diverse temperature, prescindendo dal valore assunto
a 0 °C.
Indicando con R1 e R2 i valori delle resistenze alle temperature ed applicando
l’espressione [17] si ottiene:
Facendo il rapporto tra le due espressioni e dividendo numeratore e denominatore
per si ha:





Ponendo
[21]
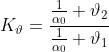
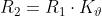

si ottiene
[22]
Il coefficiente introdotto dà anche il rapporto tra le resistività e si ha pertanto:
[23]
Di particolare importanza pratica è il caso dei conduttori in rame e in alluminio, per i
quali i valori del coefficiente di temperatura sono rispettivamente pari a 0,004264
e 0,0043
; sostituendo questi valori nella [21] si ottiene:
• rame:
[24]


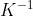
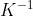

• alluminio
[25]
Facciamo qualche esempio:

Un conduttore di rame presenta, a 20 °C, la resistenza di 0,5 Ω. Calcolarne il valore
a 90 °C e determinare l’aumento percentuale della resistenza.
Applicando le formule [24] e [22] si ottiene:


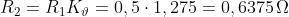
L’aumento percentuale, riferito al valore della resistenza iniziale, è dato da:
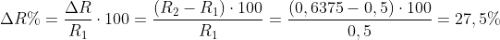

Un conduttore in alluminio presenta, a 35 °C, la resistenza di 2 Ω. Riscaldato, subisce un
aumento di resistenza del 30%. Determinare la temperatura finale

La variazione assoluta di resistenza si ricava applicando la formula inversa di quella
vista nell’esempio precedente:

La resistenza finale sarà pertanto pari a:

Ricavando dalla [22] il valore di e applicando la [25] si ottiene:
e infine :
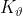




Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





