



Se volete trovare qualcosa, non c’è niente di meglio che cercare
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!





Massa
kilogrammo
kg
RESISTENZA, CONDUTTANZA, LEGGE DI OHM
Quanto sopra si può spiegare introducendo il concetto di
resistenza elettrica: il mezzo conduttore entro cui avviene il
passaggio di carica si oppone alla circolazione della corrente,
richiedendo un dispendio di energia per far sì che tale circola-
-zione avvenga.
L’energia elettrica che viene messa in gioco sarà dissipata sotto
forma di calore, come avviene, per esempio, nei conduttori di
NeI paragrafi precedenti si è visto che la tensione elettrica
tra due punti di un circuito corrisponde all’energia che occorre
fornire all’unità di carica che si sposta tra i punti suddetti.
La circolazione di carica implica il passaggio di corrente elettrica
e, quindi, vi è un rapporto di causa/effetto tra la tensione e la
corrente: per far circolare una corrente di intensità I tra due
punti di un circuito elettrico è necessario che tra questi due
punti vi sia una d.d.p. pari a V, legata all’energia fornita alla
carica
collegamento, oppure verrà trasformata in un’altra forma di energia, come succede nel caso
degli utilizzatori elettrici (lampade, motori ecc.).
Nei normali materiali conduttori la tensione necessaria a far circolare la corrente aumenta
proporzionalmente all’aumentare dell’intensità di corrente, per cui il rapporto V/I può essere
ritenuto costante e rappresenta il coefficiente di proporzionalità tra le due grandezze.
Si definisce resistenza elettrica di un circuito il rapporto tra la tensione applicata e la
corrente circolante:
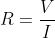
La resistenza elettrica si misura in ohm (simbolo Ω); dalla soprastante relazione si ricava la
seguente uguaglianza:

Se nella [8] si considera I = 1 A, si vede che il valore della resistenza coincide con quello
della tensione; questo consente di definire la resistenza elettrica come il valore della tensione
che occorre applicare tra due punti per ogni ampere di corrente circolante.
Supporre costante la resistenza elettrica tra due punti di un circuito significa ritenere diret-
-tamente proporzionali tra loro tensione e corrente e quindi considerare lineare la legge di
variazione V=f(I), come mostrato graficamente nella figura [9].
L’equazione della retta è data da:
[8]
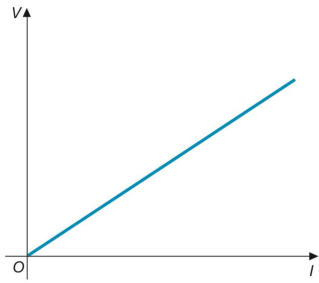

Rappresentazione grafica dell’equazione V = RI.
Influenza del valore di R nel grafico V = f (I).

ed esprime analiticamente la legge di Ohm.
Il valore della resistenza R rappresenta il coefficiente angolare della retta e ne determina
l’inclinazione: all’aumentare di R cresce, a parità di corrente, il valore della tensione e la
retta ruota in senso antiorario, come mostrato nella figura [10].
Vi sono dei casi in cui la resistenza non è costante e quindi la legge che lega
tensione e corrente non è lineare, come mostrato, per esempio, nel grafico di
figura [11]
[10]
[9]
in cui è rappresentata la caratteristica tensione-corrente di un varistore, ossia di
un elemento circuitale la cui resistenza varia con la tensione.

[11]
Caratteristica tensione-corrente
di un resistore non lineare.
Ricavando la corrente dall’equazione [9] si ottiene
la legge i = f(V):
Si definisce conduttanza elettrica, indicata con il
simbolo G, il rapporto:
In funzione della conduttanza la legge di Ohm
diventa pertanto:
[10]
La conduttanza si misura in siemens (simbolo S) e

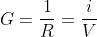

rappresenta il reciproco della resistenza: un elevato valore di G indica un piccolo valore di
resistenza e, quindi, maggior corrente circolante a parità di tensione applicata.
L’esame della [10] mostra inoltre che, considerando V = 1 V, il valore della conduttanza
coincide con quello della corrente conseguente all’applicazione della tensione unitaria.
Ad esempio calcoliamo la resistenza e la conduttanza di un circuito, sapendo che l’applica-
-zione di una tensione di 5 V determina la circolazione di una corrente pari a 20 mA.
Usando le formule viste in questo paragrafo, la risoluzione è immediata:

Resistività e conduttività
Si consideri (figura 12) un conduttore di lunghezza l e sezione S, che collega i punti A e B
di un circuito e nel quale circoli la corrente I, nel senso da A verso B.
Tale circolazione è possibile in quanto il generatore imprime al punto A un potenziale
maggiore del punto B.
Si può allora dire che vi è una diminuzione di potenziale elettrico lungo il percorso della
corrente, ossia una caduta di tensione (c.d.t.) tra i punti A e B, pari a V = Va– Vb, con un
andamento lineare, supponendo che il conduttore abbia caratteristiche omogenee in tutti i
punti.
Il raporto

[12]

Rappresentazione grafica della caduta
di tensione per unità di lunghezza

espresso in volt per metro, rappresenta allora
la c.d.t. per unità di lunghezza, essendo pari
alla caduta di tensione per ogni metro di
conduttore.
La caduta di tensione totale tra i punti A e B
sarà data da:
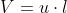
Introducendo anche la densità di corrente, la
resistenza elettrica del tratto A-B può essere
espressa nel modo seguente:
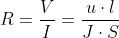
Le grandezze u e J, essendo riferite a lunghezza e sezione unitarie, non dipendono, a differ-
-enza della resistenza, dalle dimensioni del conduttore, ma soltanto dal materiale che lo
costituisce e pertanto anche il valore del loro rapporto è solo funzione delle caratteristiche del
materiale.
Il rapporto
assume il nome di resistività elettrica del materiale conduttore.
Quindi l’espressione [11] diviene:

[11]

[12]
La soprastante relazione esprime la resistenza elettrica di un conduttore in funzione delle sue
dimensioni geometriche e delle caratteristiche fisiche del materiale. Dal suo esame si possono
trarre le seguenti conclusioni:
•
all’aumentare della sezione la resistenza elettrica diminuisce in quanto, a parità di
corrente, le cariche hanno più spazio per fluire attraverso il conduttore (J diminuisce)
e quindi incontrano minore resistenza;
•
all’aumentare della lunghezza la resistenza elettrica aumenta perché diventa maggiore
la d.d.p. V = ul necessaria per far circolare la stessa corrente tra i due punti considerati;
•
la resistenza elettrica è direttamente proporzionale alla resistività del materiale conduttore,
grandezza legata alle sue caratteristiche intrinseche; per avere la minima resistenza deve
essere di piccolo valore la resistività, come avviene nei buoni conduttori (argento, rame,
alluminio);
•
il valore della resistività è pari a quello della resistenza di un conduttore avente lunghezza
e sezione unitaria.
Dalla relazione [12] si determina:

L’unità di misura della resistività si ottiene dalla soprastante relazione, a seconda delle unità
di misura usate per S e l; normalmente si ha:

In alcuni casi la sezione viene espressa in metri quadrati, ottenendo :

Dalla relazione [12] si può ricavare l’espressione della conduttanza:

La grandezza:

è detta conduttività elettrica del materiale conduttore e rappresenta l’inverso della
resistività.
La sua introduzione consente di esprimere la conduttanza in funzione delle caratteristiche
fisiche del materiale e delle dimensioni del resistore
[14]
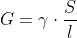
[15]
Il significato della conduttività è opposto a quello della resistività: un elevato valore di
implica, a parità di dimensioni, un elevato valore di conduttanza e quindi un basso valore di
resistenza.
Le unità di misura della conduttività elettrica si ricavano da quelle della resistività, si ottiene:



Ad esempio calcoliamo la resistenza e la conduttanza di un conduttore in rame
di lunghezza 100 m e sezione
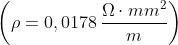

applicando le formule viste sopra:

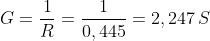
Ancora per esempio, consideriamo un filo conduttore di sezione 6 mm2 di cui si ignora il
materiale di cui è costituito; provandone in laboratorio uno spezzone di lunghezza 1 m è
stata misurata una caduta di tensione di 0,1 V facendo circolare una corrente di 5 A.
Calcoliamo la resistenza, la conduttanza, la resistività e la conduttività.
Applicando la legge di Ohm si ottengono i valori della resistenza e della
conduttanza:


Usando le espressioni [13] e [14] si ricavano i valori della resistività e della
conduttività:
[13]




Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





