Ma quando un vegetariano muore si reincarna o si 'reinverdura'

ELETTRONICA DIGITALE

… studiare, studiare ed ancora studiare, è il solo modo di capire quanto possa essere grande sia la propria ignoranza!

ALGEBRA DI BOOLE

Definizioni L’algebra di Boole, sviluppata da George Boole, matematico inglese (1815-1864), e completata in seguito da un altro matematico inglese, De Morgan (1806-1871), è un insieme di definizioni, postulati e teoremi su grandezze che possono assumere soltanto due stati logici nettamente distinti tra loro e che si escludono a vicenda. Definita anche algebra delle proposizioni logiche, poiché non tratta numeri, è lo strumento matematico su cui si basano l’analisi e la sintesi dei circuiti digitali.

Ogni grandezza booleana può assumere due stati o valori logici che si rappresentano con due simboli V (vero) e F (falso), oppure H (high) e L (low). In elettronica digitale è consuetudine adottare i due simboli 0 e 1, che non hanno significato di numeri. Una costante booleana è una grandezza che assume sempre e soltanto lo stato 0 oppure sempre e soltanto lo stato 1. Una variabile booleana è una grandezza che può assumere sia lo stato 0 sia lo stato 1. Una variabile si dice indipendente se può assumere indifferentemente uno dei due stati, dipendente se il suo valore logico dipende da altre variabili e in tal caso si dice anche che è funzione di altre variabili.

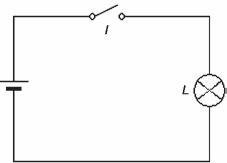
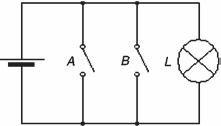
Ad esempio, nella fgra a destrea, è riportato un circuito applicativo dell’algebra booleana. L’interruttore I è una variabile booleana di tipo indipendente, poiché può essere tenuto arbitrariamente aperto (valore logico = 0) oppure chiuso (valore logico = 1). La lampada L è anch’essa una variabile booleana, poiché può assumere solo due stati, spenta (0) oppure accesa (1), ma di tipo dipendente, poiché il suo valore logico è funzione dello stato dell’interruttore I. Si ricordi che l’assegnazione dei simboli 0 e 1 è del tutto arbitraria.

Operazioni booleane elementari Nell’algebra booleana, come in quella numerica, si possono eseguire le operazioni sulle costanti e sulle variabili. Gli operatori logici elementari (o funzioni logiche elementari) sono la somma, il prodotto e la negazione (o complemento). Somma logica (OR) Le regole della somma logica (simbolo +) tra due costanti, 0 e 1, sono le seguenti: 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 1 Si definisce somma di n variabili (A, B, C, D, …) la seguente espressione: S = A + B + C + D + … (che si legge: S uguale ad A or B or C or D or …). La somma Sè uguale a 1 se almeno una delle n variabili vale 1; è uguale a 0 se tutte le n variabili valgono 0.

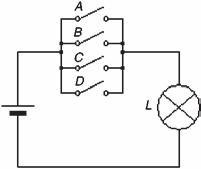
Significato fisico della somma logica

Se le variabili booleane A, B, C, D rappresentano interruttori, la somma ha il significato di collegare tutti gli interruttori in parallelo (come nella figura a lato). Infatti se alla variabile booleana interruttore si associa il valorte logico 0 per indicare l’inter- -ruttore aperto e il valore logico 1 per indicare l’interruttore chiuso, la continuità del circuito è assicurata quando almeno un interruttore è chiuso, ovvero quando almeno una delle variabili A, B, C, D vale 1.

Circuito applicativo dell’algebra booleana.

Prodotto logico (AND) Le regole del prodotto logico (simbolo ∙) tra due costanti, 0 e 1, sono: 0 · 0 = 0 0 · 1 = 0 1 · 0 = 0 1 · 1 = 1 Il prodotto logico può essere indicato sia con il punto di moltiplicazione (∙), sia con l’asterisco (*), sia con nessun simbolo (come nell’algebra numerica). Si definisce prodotto tra n variabili (A, B, C, D, …) la seguente espressione: (si legge: pi greco uguale ad A and B and C and D and …). Il prodotto Π è uguale a 1 se tutte le n variabili assumono lo stato 1; è uguale a 0 se almeno una variabile vale 0.

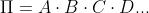
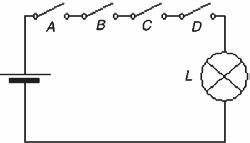
Significato fisico del prodotto logico

Se le variabili booleane A, B, C, D rappresentano interruttori, il prodotto ha il significato di collegare tutti gli interruttori in serie (come nella soprastante figura). Se alla variabile booleana interruttore si associa il valore logico 0 per indicare l’interruttore aperto e il valore logico 1 per indicare l’interruttore chiuso, la continuità del circuito è assicurata quando tutti gli interruttori sono chiusi, ovvero quando tutte le variabili booleane A, B, C, D valgono 1.

Negazione o complemento (NOT) L’operazione di negazione consiste nell’assegnare alla variabile lo stato logico opposto: Assegnata una variabile A, la sua negazione (o il complemento) è (si legge: A negato) e assume lo stato logico opposto.

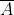
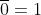
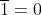
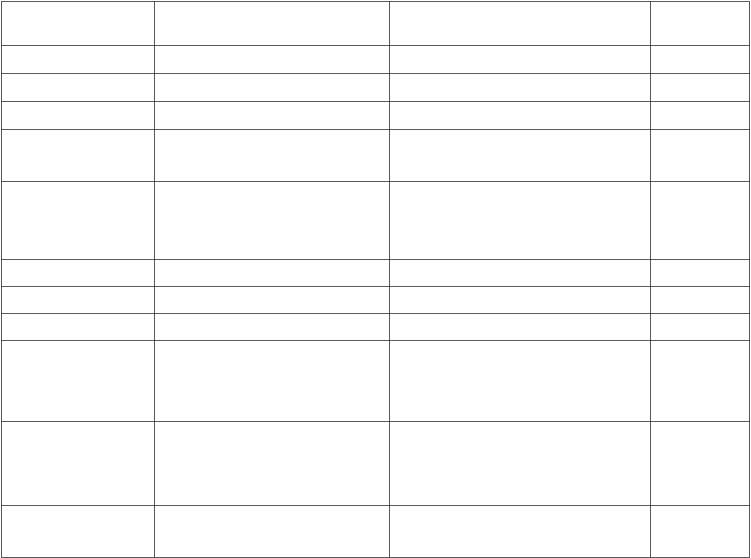
Teoremi, proprietà e regole dell’algebra booleana

Teoremi

Somma

Prodotto

Negazione

Dominanza

Idempotenza

Involuzione

Primo teorema dell’assorbimento

Secondo teorema dell’assorbimento

Complementare

Identità

Commutativa

Distributiva

Associativa

Regola di De Morgan

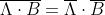
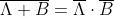
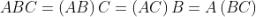
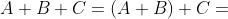
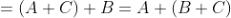
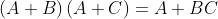
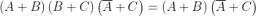
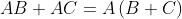
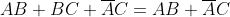
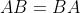
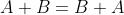
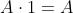
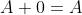
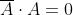
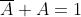
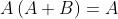
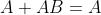
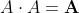
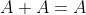
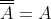
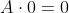
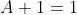
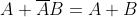
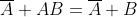
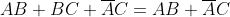
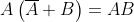
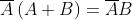
Principio della dualità Dalla soprastante tabella si deduce che tutte le espressioni della somma e del prodotto sono tra loro duali. Si può passare dalla somma al prodotto con le seguenti sostituzioni formali: • ; • ; • . Si può passare dal prodotto alla somma con le seguenti sostituzioni formali: • ; • ; • . La dualità si può verificare facilmente notando che la prima riga della AND è opposta all’ultima riga della OR; la seconda riga della AND è opposta alla penultima riga della OR, e così via. In generale si può affermare che ogni funzione espressa come somma di prodotti (SOP, Sum Of Products) ha la sua espressione duale scritta come prodotto di somme (POS, Product Of Sums).

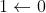
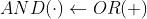
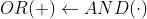
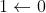
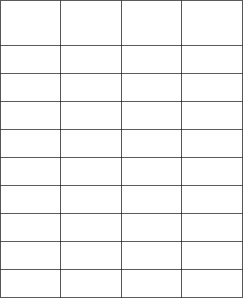
Funzioni booleane Una variabile booleana si definisce indipendente quando è possibile assegnare a essa uno qualsiasi degli stati logici. Con n variabili booleane indipendenti si possono scrivere configurazioni. Assegnate n variabili indipendenti (A, B, C, D, …) e una variabile booleana Y, se esiste una legge che fa corrispondere ad ogni configurazione delle n variabili un valore della Y, si dice che Y è funzione delle n variabili indipendenti. La Y è una variabile booleana dipendente. Con n variabili indipendenti si possono ottenere funzioni indipendenti pari a . Una funzione booleana può essere rappresentata come: • con una tabella (o tavola) di verità; • in forma analitica; • con le mappe di Karnaugh. A differenza degli interruttori, che possono essere tenuti arbitrariamente aperti o chiusi, e quindi rappresentano variabili booleane indipendenti, la lampada è accesa o spenta in funzione dello stato degli interruttori, e rappresenta una variabile booleana dipendente.

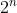
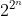
Tabella (o tavola) di verità La tabella (o tavola) di verità è una rappresentazione grafica della funzione booleana. Nella tabella a fianco è riportato un esempio di tabella di verità con tre variabili indipendenti. Per convenzione le variabili indipendenti vanno scritte a sinistra, la variabile (o le variabili) dipendente (o dipendenti) a destra. Per scrivere tutte le combinazioni in modo ordinato si assegnano i pesi alle variabili come nel sistema di numerazione binario. Per ogni possibile configurazione la rappresentazione definisce il valore della funzione. In tabella alla y sono stati assegnati valori casuali, norma- -lmente tali valori si deducono dalle specifiche del problema da risolvere. Si dice che la funzione di uscita è vera quando y = 1 e che è falsa quando y = 0.

Esempio di tabella della verità di una funzione a tre variabili.

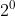
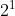
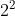
Rappresentazione analitica Una funzione booleana può essere rappresentata in forma analitica utilizzando le tre operazioni elementari AND, OR, NOT. Il mintermine (termine minimo): • è il prodotto logico delle variabili indipendenti; ogni variabile viene scritta in modo diretto se vale 1, in modo negato se vale 0; • è così chiamato perché un solo termine prodotto rende vera la funzione; • è uno delle configurazioni in cui possono esistere le variabili d’ingresso. Il maxtermine (termine massimo): • è una somma logica in cui compaiono le variabili indipendenti di una funzione booleana; ogni variabile viene scritta in modo diretto se vale 0, in modo negato se vale 1; • è uno delle configurazioni in cui possono esistere le variabili d’ingresso; • è così chiamato perché un solo termine somma di valore 0 rende massimo il numero di 1 della funzione. Nella tab. 16.25 sono riportati i mintermini e maxtermini di una funzione a tre variabili. La forma di mintermini (SOP) è una espressione algebrica costi- -tuita dalla somma di tutti i minte- -rmini che rendono vera la funzio- -ne (y = 1). La forma di maxtermini (POS)è una espressione algebrica costitu- -ita dal prodotto di tutti i maxter- -mini che rendono falsa la funzio- ne (y = 0). È possibile passare da una forma all’altra svolgendo le operazioni e applicando le proprietà algeb- -riche. In generale la forma più utilizzata è quella di mintermini perché gli 1 della funzione sono in numero inferiore agli 0. La forma canonica è una espressione algebrica standard con la quale può essere scritta una funzione logica. È canonica perché ogni termine (prodotto o somma) contiene tutte le variabili indipendenti. Un’espressione booleana può essere scritta sotto forma canonica di mintermini ovvero sotto forma canonica di maxtermini. Se i prodotti o le somme non contengono tutte le variabili (perché la funzione è stata semplificata), la forma SOP o POS non è più canonica. Le forme standard consentono di realizzare una funzione con circuiti logici a due livelli: AND-OR oppure OR-AND.

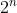
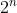
Mintermini e maxtermini per una funzione a tre variabili.

Minter- mine

Simbolo minter- mine

Maxterm- ine

Simbolo maxterm- ine

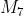
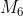
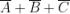
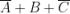
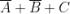
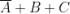
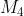
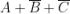
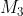
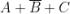
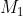
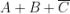
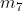
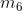
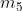
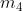
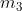
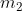
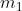
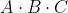
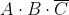
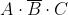
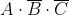
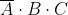
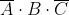
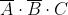
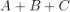
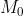
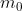
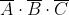
Ad esempio, considerando la soprastante tabella della verità di una funzione a tre variabili, si suppone di voler scrivere in forma canonica di mintermini e di maxtermini la funzione logica riportata nella detta tabella di verità e di voler passare da una forma all’altra. I mintermini che rendono vera la funzione (Y = 1) sono i seguenti: La forma canonica di mintermini è la somma dei prodotti in corrispondenza dei quali la funzione assume valore 1, quindi la sua espressione è la seguente: I maxtermini che rendono falsa la funzione (Y = 0) sono i seguenti: La forma canonica di maxtermini è il prodotto delle somme in corrispondenza delle quali la funzione assume valore 0, quindi la sua espressione dedotta direttamente dalla tabella di verità in esame è la seguente: Svolgendo i prodotti e applicando i teoremi, le proprietà e le regole riportate nella soprastante tabella, si ha: I termini mancanti di una variabile, come per esempio a b, sottintendono due termini: ; perciò y diventa:

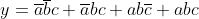
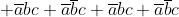
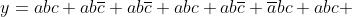
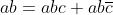
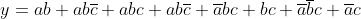
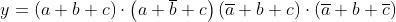
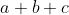
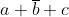
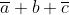
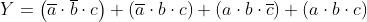
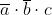
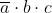
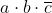
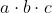
Mappe di Karnaugh Le mappe di Karnaugh costituiscono sia un metodo di rappresentazione grafica sia un metodo di semplificazione di una funzione espressa in forma SOP o POS. La mappa è un insieme di celle; ogni cella rappresenta un mintermine o un maxtermine della funzione. Con n è stato indicato il numero di variabili indipendenti. Il metodo è valido per n ≤ 5; per n > 5 diventa complesso e poco efficace. 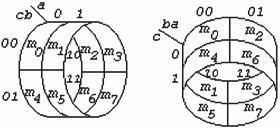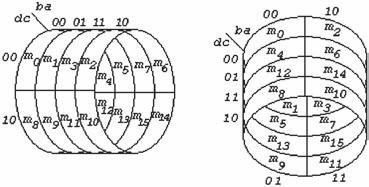La mappa è un diagramma a due dimensioni e ha come coordinate orizzontali e verticali le variabili indipendenti. Nelle soprastanti figure (a), (b), ( c) e (d) sono disegnate le mappe a due, a tre e a quattro variabili. Per le espressioni a tre variabili la mappa può essere verticale (figura b) oppure orizzontale (figura c). In ogni cella è indicato, per maggiore chiarezza, il mintermine corrispondente. La corrispondenza tra simbolo e configurazione è indicata nela tabella a lato, nella quale è stata considerata a la variabile meno significativa e d quella più significativa. La rappresentazione di una funzione booleana sulla mappa consiste nel porre un bit 1 nelle celle i cui mintermini rendono vera la funzione (y = 1). È superfluo riportare gli 0. Le mappe per le funzioni a cinque variabili sono costituite da due mappe a quattro variabili, ciascuna valida per un valore differente della quinta variabile.

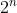
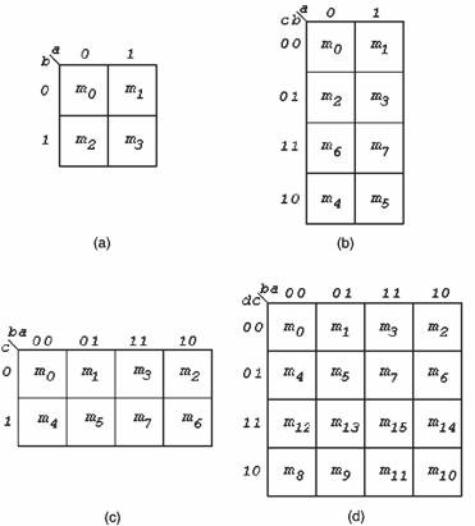
Corrispondenza tra simbolo e configurazione delle variabili indipendenti

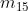
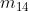
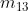
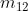
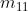
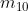
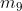
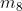
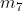
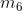
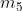
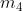
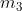
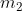
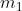
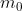
Ad esempio, si vuole rappresentare sulla mappa di Karnaugh la funzione a tre variabili assegnata con la sottostante tabella di verità di . Per facilitare il posizionamento degli 1 è opportuno tradur- -re ciascuna configurazione nel corrispondente numero decimale, come riportato nella tabel- -la, segnare i decimali che generano y =1 e individuare sulla mappa la cella con il minte- -rmine avente come pedice lo stesso numero decimale. La rappresentazione della funzione e la relativa semplificazione (confrontare il metodo di minimizzazione con il metodo delle mappe) non sono dipendenti dal tipo di mappa, verticale o orizzontale, adottato.

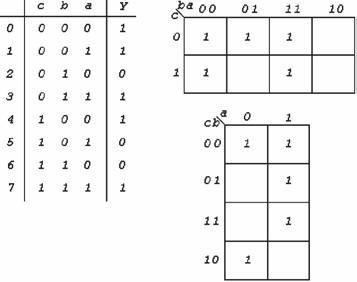
Rappresentazione di una funzione a tre variabili con la tabella e con la mappa.

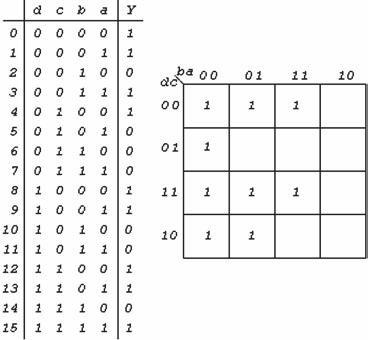
Rappresentazione di una funzione a quattro variabili con la tabella e con la mappa.

Sempre per esempio Si voglia rappresentare sulla mappa di Karnaugh la funzione a quat- -tro variabili assegnata con la tabella di verità della sottostante figura a lato. Per facilitare il posizionamento degli 1 è opportuno tradurre ciascuna configura- -zione nel corrispondente numero decimale, come riportato nella tabella, segnare i decimali che generano y = 1 e individuare sulla mappa la cella con il mintermine avente come pedice lo stesso numero decimale.

Condizioni non specificate Può accadere a volte che il valore della funzione in corrispondenza di alcune configurazioni d’ingresso non sia specificato perché non interessa, ovvero perché quelle configurazioni non sono fisicamente realizzabili. In questo caso si parla di condizioni non specificate o di indifferenza (don’t care conditions) perché appunto è indifferente il valore assunto dalla funzione. Tali condizioni potrebbero essere utili nella semplificazione (minimizzazione) di una espressione booleana in quanto, se opportuno, sono da considerare come 1; in questo modo contribuiscono ad aumentare le dimensioni del blocco di semplificazione portando così ad una maggiore minimizzazione. Sulle mappe le condizioni di indifferenza sono segnate con una X.

Operazioni universali In algebra booleana oltre alle operazioni logiche elementari (AND, OR, NOT) esistono operazioni logiche, chiamate universali. Un’operazione si definisce universale perché è in grado da sola di esprimere una funzione booleana senza le operazioni logiche elementari. Pertanto un circuito combinatorio può essere implementato con sole porte universali. L’implementazione di un circuito combinatorio con porte universali può essere un’altra tecnica di minimizzazione di una funzione booleana. Le operazioni universali sono NAND e NOR.

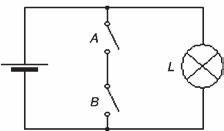
NAND L’operazione universale NAND tra due variabili A e B è la negazione del loro prodotto. NAND è la sintesi di NOTAND. L’operazione NAND consente di scrivere una espressione in forma SOP sostituendo tutte le operazioni elementari AND, OR e NOT, quindi il circuito combinatorio che implementa la funzione è costituito da sole porte NAND. L’operazione NAND tra due variabili si legge A NAND B. La NAND è l’operazione duale della NOR. Nella tabella a lato sono riportate le regole dell’operazione e sotto il suo significato fisico. Alcune fondamentali proprietà dell’operazione NAND sono: • (proprietà commutativa); • Non gode della proprietà associativa; • (si legge A NAND se stesso); • ; • ; • ;

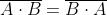
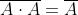
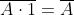
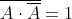
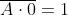
Tabella di verità della funzione NAND

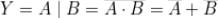
NOR L’operazione universale NOR tra due variabili A e B è la negazione della loro somma. NOR è la sintesi di NOT-OR. L’operazione NOR consente di scrivere un’espressione in forma POS sostituendo tutte le operazioni elementari AND, OR e NOT. Un circuito combinatorio implementato con sole porte NOR può impiegare meno integrati rispetto alla realizzazione con porte AND, OR e NOT. L’operazione NOR tra due variabili si legge A NOR B. La NOR è l’operazione duale della NAND. Nella tabella a lato sono riportate le regole dell’operazione e sotto il suo significato fisico. Alcune fondamentali proprietà dell’operazione NOR sono: • (proprietà commutativa); • Non gode della proprietà associativa; • ; • (si legge A NOR se stesso); • ; • .

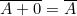
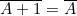
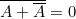
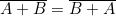
Tabella di verità della funzione NOR

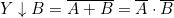
Metodi di minimizzazione di una funzione booleana Una funzione si dice minimizzata (o semplificata) quando contiene il minor numero possibile di variabili d’ingresso e di termini. Un’espressione minimizzata richiede per la sua implementazione il minor numero possibile di porte logiche e quindi di circuiti integrati. La semplificazione di una funzione consiste nel trasformare l’espressione data in una equivalente, scritta in una forma minima. La funzione minimizzata, con un metodo qualsiasi, quindi non più in forma canonica, espressa in forma SOP o POS, non è unica e in genere vi sono più alternative. La minimizzazione di un’espressione si ottiene più semplicemente utilizzando le mappe di Karnaugh.

Metodo delle mappe di Karnaugh Il metodo di semplificazione con le mappe di Karnaugh è valido quando il numero delle variabili n ≤ 5. Altri svantaggi delle mappe sono i seguenti: • all’aumentare del numero delle variabili, il metodo diventa piuttosto lungo e quindi non privo di errori; vi sono tuttavia in commercio alcuni software che con il supporto del computer facilitano il compito; • a volte la semplificazione non è delle migliori e risulta più conveniente semplificare utilizzando la funzione XOR. È necessario sottolineare anche che il compito del progettista è più orientato a utilizzare i circuiti integrati esistenti in commercio ovvero all’utilizzo e alla programmazione dei PLD. La progettazione di un circuito combinatorio con questa tecnica è davvero molto limitata. Le mappe sono costruite in modo tale che le celle adiacenti, cioè separate con un lato da quelle vicine, sono a distanza unitaria. Infatti, nel passaggio da una cella all’altra, sia in senso verticale sia in senso orizzontale, cambia un solo bit. La proprietà di distanza unitaria è rispettata anche dalle celle delle righe e delle colonne estreme. Pertanto le mappe devono essere pensate come se fossero piegate su se stesse in modo tale da formare un cilindro orizzontale e uno verticale. A lato sono disegnate le mappe per le funzioni a tre variabili e sotto per quelle a quattro variabili. Per la semplificazione le regole sono le seguenti: • tutte le celle adiacenti contenenti gli 1 vanno raggruppate in un unico blocco; • su una mappa possono esserci più blocchi; • il numero di blocchi deve essere il minore possibile; • il blocco deve essere quanto più grande possibile; • il blocco deve avere forma quadrata o rettangolare; • il blocco deve essere costituito da un numero di celle potenza di 2; • ogni cella contenente un 1 deve essere presa almeno una volta, quindi una cella può far parte di più blocchi; • se una cella contenente un 1 non ha altri 1 adiacenti, deve essere presa singolarmente; • per le funzioni a cinque variabili, sono da considerarsi adiacenti (quindi a distanza 1) i blocchi e le celle che coincidono sovrapponendo le due mappe da quattro variabili. Per passare dalla mappa alla forma analitica minimizzata della funzione è necessario far corrispondere a ogni blocco un prodotto delle variabili che non cambiano valore percor- -rendo il blocco sia in senso verticale sia in senso orizzontale. La forma analitica della funzione è del tipo SOP, ma non canonica. Il metodo della mappa di Karnaugh può essere applicato anche alla forma POS della funzione booleana. In questo caso devono essere riportati gli 0 e applicate le stesse regole viste precedente- -mente. È conveniente utilizzare questa forma quando gli 0 sono in numero inferiore agli 1, ovvero quando è più facile creare i blocchi di semplificazione con gli 0.

Se, ad esempio, si vuole semplificare l’espressione Si nota che la funzione è a quattro variabili, cioè dcba, con d di peso maggiore e a di peso minore; la mappa di Karnaugh con il posiziona- -mento dei mintermini è indicata a lato. Consideriamo i singoli blocchi e i termini a essi associati. Percorrendo ciascun blocco in verticale e oriz- -zontale si eliminano le variabili che cambiano di valore. I risultati trovati sono i seguenti: • blocco 1: ; • blocco 2: ; • blocco 3: ; • blocco 4: . La funzione minimizzata in forma SOP è

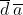
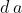
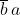
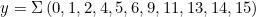
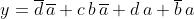
Mappa di Karnaugh per la semplificazione dell’espressione dell’esempio

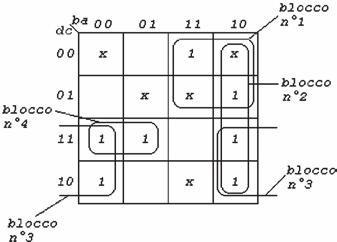
Adesso si vuole semplificare la funzione assegnata con la tabella di verità riportata nella tabella a lato. La funzione contiene alcune configurazioni non specificate che vanno riportate sulla mappa come gli 1 perché potrebbero essere utili per la semplificazione. Nell’individuare i blocchi di semplificazione (vedi sottostante mappa) sono state prese alcune configurazioni non specificate come 1, altre invece sono state trascurate, quindi sono state considerate come di valore 0. Dai blocchi derivano i seguenti termini: • blocco 1: • blocco 2: • blocco 3: • blocco 4:

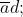
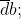
Corrispondenza tra simbolo e configurazione delle variabili indipendenti

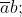
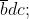
È utile ricordare che la forma minima della funzione non è unica, si possono prendere in considerazione blocchi diversi da quelli scelti.

Consideriamo di utilizzare la mappa di Karnaugh per minimizzare l’espressione in forma POS: Sono stati scelti i blocchi di semplificazione mostrati nella sottostante figura, dai quali derivano i seguenti termini: • blocco 1: c + b; • blocco 2: b + a. La funzione così semplificata è

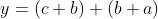
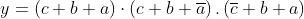
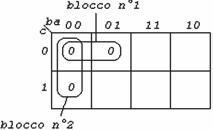
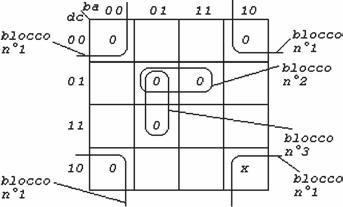
Minimizzare la funzione in forma POS indicata nella tabella a lato. Poiché la funzione è data in forma POS, devono essere riportati sulla mappa gli 0 e non gli 1. Anche in questo caso le condizioni di indifferenza possono essere utili per minimizzare ulteriormente l’espressione della sottostante mappa. Dai blocchi presi in considerazione i termini ottenuti sono i seguenti: • blocco 1: • blocco 2: • blocco 3: La funzione minimizzata è

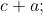
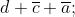
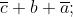
Tabella di verità della funzione in esempio

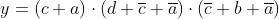
Mappa di Karnaugh per la semplificazione della funzione dell’esempio

Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara

Home