



Anche una spina è gradita quando poi ci si aspetta di vedere una rosa
ELETTRONICA DIGITALE
… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!
SISTEMI DI NUMERAZIONE




Vengono di seguito riportate alcune tabelle con le unità di
misura più ricorrenti in elettronica digitale.
Le unità di misura sono in:
Unità di misura per il trasferimento dei dati


Simbolo
Unità di misura
Descrizione
Bd
Baud
1 bit per secondo (1bps)
bps
Bit per secondo
Velocità di trasferimento dei dati tra
computer
MIPS
Milioni di istruzioni
per secondo
Quantità di istruzioni elementari della
CPU elaborate nell’unità di
tempo(secondo) nella CPU
Hz
Hertz
Unità di misura della frequenza

Unità di misura per la visualizzazione
di una immagine


Simbolo
Unità di
misura
Descrizione
dpi
Dots per
inch
Quantità di punti per pollice
quadrato (2,54 ×2,54 cm) in
una immagine
px
Pixel
Puntino luminoso, identifica
la risoluzione di un monitor

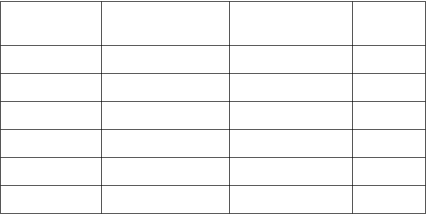
Unità di misura per la memorizzazione dei dati


Simbolo
Unità di misura
(bit)
Unità di
misura(Byte)
Potenza
di2
bit
1
1/8
Byte
8
1
KB (kilobyte)
8192
1024
MB (megabyte)
8 388 608
1 048 576
GB (gigabyte)
8 589 934 592
1 073 741 824
TB (terabyte)
8 796 093 302 400
1 099 511 628 000

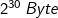





Sistema di numerazione binario
Il sistema di numerazione binario ha base 2: base 2 = (0, 1)
Ogni cifra prende il nome di bit (binary digit).
L’utilizzo del sistema di numerazione binario è dovuto alla possibilità di legare facilmente
i bit agli stati di funzionamento dei circuiti elettronici.
L’inconveniente è invece dovuto al fatto che, più piccola
è la base, più cifre ha il numero.
Seguendo le stesse regole del sistema di numerazione
decimale, il conteggio binario si esegue nel modo indicato
nella tabella a lato.
Meccanismo di conteggio
del sistema binario

000
101
001
110
010
111
011
1000
100
....

Sistema di numerazione esadecimale
La base di un sistema di numerazione esadecimale è
costituita da 16 simboli alfanumerici:
base 16 = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F)
Il sistema di numerazione esadecimale è utile per scrivere
i numeri binari molto lunghi in forma più breve.
A ogni cifra esadecimale corrispondono quattro bit.
In analogia con tutti gli altri sistemi di numerazione, il
processo di conteggio segue lo stesso meccanismo che
viene riportato nella tabella a destra.
Anche i numeri del sistema esadecimale possono essere
scritti mediante espansione di potenze di 16.
Il valore posizionale delle cifre è legato alle potenze di 16.
Meccanismo di conteggio
del sistema esadecimale

0
1B
1
1C
2
1D
…
1E
8
1F
9
20
A
21
B
22
C
…
D
28
E
29
F
2A
10
2B
11
…
12
2E
…
2F
18
30
19
31
1A
....

Conversione tra sistemi di numerazione
La conversione è quell’operazione che consiste nello
scrivere un numero in un altro sistema di numerazione.
La conversione dei numeri interi si esegue dividendo il
numero per la base del sistema di numerazione di arrivo
fino a ottenere un quoziente nullo.
I resti costituiscono il numero convertito.
L’ultimo resto è la cifra più significativa, il primo resto è
la cifra meno significativa.
La conversione dei numeri frazionari si esegue invece
moltiplicando il numero da convertire per la base del
sistema di numerazione di arrivo.
Le parti intere dei prodotti rappresentano il numero
convertito. La parte intera del primo prodotto costituisce
la cifra più significativa, la parte intera dell’ultimo prodot-
-to è invece la cifra meno significativa.
Conversione decimale/esadecimale
Per effettuare la conversione decimale / esadecimale dei numeri interi si divide il numero
per 16 fino ad ottenere un quoziente nullo.
I resti formano il numero convertito nella base 16.
Per convertire i numeri frazionari si moltiplica il numero per 16.
La parte intera costituisce la cifra esadecimale.
La parte frazionaria del risultato va moltiplicata ancora per 16.
L’operazione ha termine quando la parte frazionaria del prodotto è nulla.
Se la parte frazionaria del prodotto non si annulla mai, la conversione è approssimata e
viene fermata quando si ritiene che l’errore sia accettabile.
Conversione decimale/binario
Per eseguire la conversione decimale / binario dei numeri interi si possono usare due
metodi:
•
divisioni successive fino ad ottenere quoziente nullo; i resti, che possono essere 0 o 1,
costituiscono il dato binario;
•
si predispone una tabella con le potenze di 2 (vedi la sottostante tabella) e si posizio-
-nano gli 1 nelle caselle corrispondenti in modo da formare il numero decimale
assegnato
Tabella delle potenze di 2

Potenze di 2
Numero decimale corrispondente alle potenze
di 2
256
128
64
32
16
8
4
2
1
Numero decimale convertito in binario





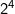
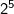



Conversione binario/decimale
Per la conversione binario / decimale dei numeri interi si possono usare due metodi:
•
espansione secondo potenze di 2; si può facilitare l’operazione predisponendo una
tabella delle potenze di 2;
•
partendo da sinistra si moltiplica per 2 il bit e il risultato si somma alla cifra successiva,
così via fino alla cifra meno significativa (più a destra).
Conversione binario/esadecimale
La conversione binario/esadecimale di numeri interi, si esegue dividendo il numero binario
in gruppi di quattro bit partendo da destra verso sinistra.
Se i bit non sono multipli di quattro, si possono aggiungere 0 non significativi per comple-
-tare i raggruppamenti.
Ogni gruppo va convertito nella corrispondente cifra esadecimale.
Conversione esadecimale/binario
Il metodo per realizzare la conversione esadecimale/binario consiste nello scrivere ogni
cifra esadecimale in binario su quattro bit.
Rappresentazione dei numeri relativi nel sistema binario
Nel sistema di numerazione binario, i numeri positivi sono sempre rappresentati con
un bit di segno uguale a 0 nella posizione più significativa seguito dai bit del modulo;
i numeri negativi invece possono essere rappresentati in tre modi differenti:
•
con modulo e segno;
•
con complemento a uno;
•
con complemento a due.
•
Rappresentazione con modulo e segno
In questo tipo di rappresentazione i numeri negativi si scrivono con un bit di segno uguale
a 1 nella posizione più significativa, seguito dai bit del modulo.
Se si dispone di quattro bit per indicare un numero relativo, è possibile rappresentare i
numeri da +7 a ‒7, come indicato nella tabella a destra.
Questo metodo ha scarso interesse applicativo poiché, oltre
ad avere l’inconveniente dello 0 positivo e dello 0 negativo,
necessita di circuiti dedicati per l’esecuzione della sottrazione.
Per risolvere più agevolmente questa operazione sono più
convenienti le rappresentazioni in complemento a 1 e in
complemento a 2
Rappresentazione con 4 bit
dei numeri binari relativi con
modulo e segno.




Numeri binari
relativi
Numeri
decimali
corrispondenti
0 111
+7
0 110
+6
0 101
+5
0 100
+4
0 011
+3
0 010
+2
0 001
+1
0 000
+0
1 000
-0
1 001
-1
1 010
-2
1 011
-3
1 100
-4
1 101
-5
1 110
-6
1 111
-7

Rappresentazione in complemento a 1
Si definisce complemento a 1 (C1) di un numero binario N,
composto da n bit, il seguente numero:

Il complemento a 1 di un numero binario si ottiene anche
semplicemente invertendo ogni bit del numero N assegnato.
La convenzione per la rappresentazione dei numeri binari
relativi in complemento a 1 (vedi la sottostante tabella) è la
seguente:
•
i numeri binari positivi si scrivono con il loro modulo ed
un bit di segno uguale a 0 nella posizione più significativa;
•
i numeri binari negativi si rappresentano con un bit di segno
uguale a 1 nella posizione più significativa ed il modulo con
il complemento a 1.
Anche in questo tipo di rappresentazione è presente l’inconve-
-niente dello 0 positivo e dello 0 negativo.
Rappresentazione dei numeri
binari in complemento a 1.




Numeri binari
relativi
Numeri
decimali
corrispondenti
0 111
+7
0 110
+6
0 101
+5
0 100
+4
0 011
+3
0 010
+2
0 001
+1
0 000
+0
1 111
-0
1 110
-1
1 101
-2
1 100
-3
1 011
-4
1 010
-5
1 001
-6
1 000
-7

Rappresentazione in complemento a 2
Si definisce complemento a 2 (C2) di un numero binario N,
composto da n bit, il seguente numero:
Il complemento a 2 di un numero binario si può determinare
sommando un 1 al complemento a 1:
La convenzione per la rappresentazione dei numeri binari
relativi (come nella sottostante tabella) in complemento a due
ha le seguenti regole:
•
i numeri binari positivi si rappre-
-sentano con il loro modulo e
un bit di segno uguale a 0 nella
posizione più significativa;
•
i numeri binari negativi si scrivono
con un bit di segno uguale
a 1 nella posizione più significativa
ed in complemento a 2.


Rappresentazione dei numeri
binari in complemento a 2.



Numeri binari
relativi
Numeri
decimali
corrispondenti
0 111
+7
0 110
+6
0 101
+5
0 100
+4
0 011
+3
0 010
+2
0 001
+1
0 000
+0
1 111
-1
1 110
-2
1 101
-3
1 100
-4
1 011
-5
1 010
-6
1 001
-7
1 000
-8

In questo tipo di rappresentazione non
vi è l’inconveniente dello 0 positivo e
dello 0 negativo e con quattro bit si
possono scrivere i numeri da +7 a −8.
Quando un numero è rappresentato in
complemento a 1 o a 2 è sempre un
numero negativo.
Le quattro operazioni nel sistema binario
Le quattro operazioni nel sistema binario seguono le stesse
regole, riportate nelle sottostanti tabelle, di quelle corrispondenti
del sistema decimale. Moltiplicare per in binario equivale
a spostare la virgola di un posto verso destra o aggiungere
uno 0 per i numeri interi. Analogamente dividere per
equivale a spostare la virgola di un posto verso sinistra.


Regole delle 4 operazioni in binario.


Addendi
Risultato
Riporto (carry)
0+0
=0
0
0+1
=1
0
1+0
=1
0
1+1
=0
1
1+1+1
=1
1
SOMMA

.


Minuendo-
Sottraendo
Risultato
Prestito
(borrow)
0-0
=0
0
0-1
=1
1
1-0
=1
0
1-1
=0
0

SOTTRAZIONE

.


Fattori
Risultato
0x0
=0
0x1
=0
1x0
=0
1x1
=1

PRODOTTO

.


Fattori
Risultato
0:1
=0
1:1
=1

Divisione

Somma algebrica con complemento a 1 e complemento a 2
Nei sistemi digitali per le sottrazioni vengono utilizzati gli stessi circuiti delle somme
convertendo i numeri negativi nel loro complemento (a 1 o a 2).
Anche il risultato è fornito nella convenzione adottata:
se positivo, ha un bit di segno uguale a 0 e un modulo, se è negativo è in
complemento a 1 o a 2.
Se si adotta la convenzione del complemento a 1, in caso di overflow del risultato è
necessaria la correzione EAC (End Around Carry) che consiste nel sommare il bit di
overflow al dato ottenuto dalla somma.
Con il complemento a 2 invece non è necessaria l’operazione EAC poiché il bit di overflow
va semplicemente ignorato.
Il complemento a 2 è più vantaggioso rispetto al complemento a 1 perché:
•
a parità di bit si possono rappresentare più numeri (ad esempio con tre bit si va da
‒8 a +7, mentre in complemento a 1 si va da ‒7 a +7);
•
esiste uno 0 solo, mentre nel complemento a 1 ce ne sono due, uno 0 positivo ed uno
0 negativo;
•
non è necessaria l’operazione EAC, indispensabile invece nel complemento a 1.


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





