Amare e’ cosi’ breve, e dimenticare cosi’ lungo

ELETTRONICA DIGITALE

… studiare, studiare ed ancora studiare, è il solo modo di capire quanto possa essere grande sia la propria ignoranza!

I CONTATORI

I contatori sono circuiti sequenziali in grado di fornire all’uscita il numero degli impulsi inviati all’ingresso di clock. Sono molto versatili: il loro campo di applicazione è ampio e particolarmente importante e va dal settore degli strumenti digitali a quello dei sistemi di temporizzazione. Sono utilizzati nei frequenzimetri, nei contagiri, nei comuni orologi digitali per la misura del tempo e più in generale nella misura di intervalli di tempo. Nei sistemi digitali, oltre all’impiego come circuiti di conteggio, sono usati come divisori o riduttori di frequenza (frequency divider o frequency scaler); sono utilizzati anche per la realizzazione

ciclica di operazioni, come per esempio l’esecuzione sequenziale delle istruzioni di un programma, la generazione di una successione prefissata di parole, ecc

Sul piano applicativo rivestono particolare importanza solo i contatori che elaborano i dati d’ingresso nel sistema di numerazione binario; comunque, a partire da questi, si possono eseguire conteggi in qualsiasi sistema di numerazione: decimale, esadecimale, ottale, ses- -sagesimale (base 60) per il conteggio dei minuti e dei secondi. Il risultato del conteggio avente un formato binario può essere inviato a: • un altro circuito digitale; • un sistema di decodifica per essere letto da un operatore. I contatori possono effettuare il conteggio in avanti (up counter), all’indietro (down counter), avanti/indietro (up/down counter). Da un punto di vista strutturale i contatori sono realizzati con flip-flop temporizzati di tipo T, ovvero con flip-flop SR e JK con funzione di trigger.

Caratteristiche e classificazione Il contatore più semplice è il flip-flop T perché è in grado di contare un solo impulso. Un contatore a n bit è costituito da un insieme di n flip-flop dalle cui uscite viene rilevato il numero degli impulsi dati in ingresso. Il contatore ha un ingresso principale, che è l’ingresso di clock ed un numero di uscite che dipende dalla grandezza del dato secondo il codice binario prescelto. Ogni qualvolta un impulso di clock entra in ingresso, il conteggio evolve molto spesso secondo il sistema di numerazione binario in altri casi secondo il codice scelto. Il segnale d’ingresso non deve essere necessariamente periodico anche se è il tipo di segnale normalmente adottato come riferimento. Si definisce modulo M di un contatore la sequenza periodica delle possibili configurazioni: M ≤ 2n, , dove n è il numero di flip-flop. Un contatore si definisce a sequenza piena (o modulo pieno) se ha modulo M ≤ 2n dove n è , utilizzando n flip-flop, è in grado di assumere tutte le possibili configurazioni. Un contatore con modulo M conta M − 1 impulsi. La codifica dei segnali di uscita serve a conoscere quale configurazione sta attraversando il circuito ed in quale successione tali combinazioni si susseguono. Molto frequentemente le uscite sono pesate secondo il sistema di numerazione binario poiché è questo il codice adottato ma è usato spesso anche il codice BCD (8421) per il conteggio decimale (da 0 a 9).

La codifica degli stati non ha invece rilevanza se il contatore è usato come divisore di frequenza poiché l’uscita che interessa è costituita da una sola linea. Un altro problema fondamentale è la decodifica degli stati sia se il risultato deve essere visualizzato (ad esempio, con un decoder/driver ed un display a 7 segmenti) sia se il contatore deve pilotare un’altra rete logica. Il circuito decodificatore, di solito un integrato MSI, decodifica gli stati in linee 1 su m; in questa operazione i codici binario naturale e BCD sono tra i più facili da trattare. La decodifica non riveste alcuna importanza se il contatore viene utilizzato come divisore di frequenza. Se alcune configurazioni non sono possibili, si dice che il contatore ha modulo M < 2n e si definisce a sequenza troncata. Per esempio se in un contatore modulo 16 la sequenza di conteggio viene fermata a 1001, si ottiene un contatore decadico, ossia modulo 10. Un contatore si definisce sincrono quando il segnale di conteggio è applicato agli ingressi di tutti i flip-flop e le loro eventuali commutazioni avvengono contemporaneamente come mostrato nella sottostante struttura circuitale. Struttura di un contatore sincrono. Un contatore è asincrono (o ripple clock) quando gli impulsi di conteggio comandano soltanto il primo flip-flop della catena e le eventuali commutazioni dei flip-flop si succedono in sequenza, come nella sottostante figura. Struttura di un contatore asincrono. Un contatore è azzerabile se è possibile forzare le uscite dei flip-flop nella posizione zero, sempre che zero faccia parte della sua sequenza di conteggio. Un contatore si definisce programmabile se è possibile inizializzarlo da una qualsiasi configurazione che fa parte della sequenza di conteggio.

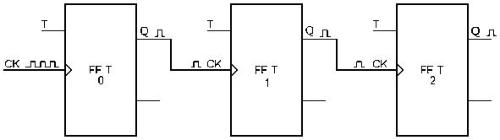
Contatori asincroni I contatori asincroni sono chiamati anche contatori a propagazione di comando (ripple clock counters) proprio per indicare che il segnale di clock si propaga nella catena dei flip-flop come un’onda lungo una corda (si veda la sotostante figura).

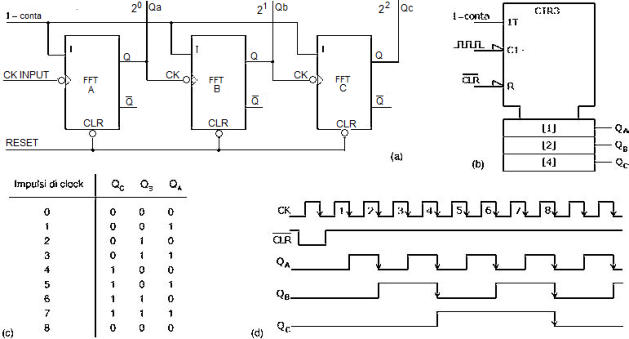
Per la realizzazione dei contatori asincroni è essenziale il fronte di commutazione dei flip-flop.

Contatore asincrono, in avanti (up), modulo 8: (a) realizzazione con flip-flop T di tipo NET, (b) simbolo logico, (c) tabella degli stati, (d) diagramma dei tempi.

Contatori asincroni in avanti con I contatori asincroni con sono i più semplici costruttivamente e si possono realizzare con flip-flop T, JK o SR configurati come T, comunque tutti temporizzati. Nella soprastante figura (a) è riprodotto lo schema circuitale e in figura (b) il simbolo logico di un contatore asincrono in avanti con modulo pieno realizzato con tre flip-flop T negative edge triggered. Vediamone il funzionamento. Un livello logico basso sull’ingresso RESET forza le uscite dei flip-flop T a zero, portando così il circuito nello stato di partenza 000; con RESET disattivo può avere inizio il conteggio. Il flip-flop A commuta sul fronte di discesa del primo impulso di clock, quindi la sua uscita si porta a livello 1. La transizione basso/alto di QA non produce alcun effetto sul flip-flop B che resta bloccato, lo stesso vale per il flipflop C. Dopo il primo impulso in ingresso lo stato del contatore è 001 (in figura C è riportata la tabella degli stati e in figura D il diagramma dei tempi). Sul fronte negativo del secondo impulso l’uscita del flip-flop A passa da 1 a 0, causando così la commutazione del flip-flop B. Il terzo flip-flop è ancora bloccato. Dopo il secondo impulso di clock l’uscita del contatore è 010. Con i successivi impulsi la rete sequenziale percorre tutta la sequenza periodica delle configurazioni secondo il codice binario naturale. Il circuito può esistere in tutti gli 8 stati e conta fino a 7 impulsi. L’ottavo segnale di clock riporta il circuito nella condizione di partenza 000. Si può facilmente osservare che ad ogni uscita dei vari flip-flop è associato un peso e, come nel sistema di numerazione binario, la loro variazione è funzione delle potenze di 2. Nel caso in cui si utilizzano flip-flop T che commutano sul fronte positivo del clock, sono i segnali Q che devono comandare i flip-flop successivi mentre le uscite dati restano invariate. Il nuovo circuito è riportato nella figura a lato ed il relativo diagramma dei tempi mostrato nella figura (b).

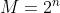
Contatore asincrono, in avanti, modulo 8: (a) realizzazione con flip-flop T di tipo PET, (b) diagramma dei tempi.

Contatore asincrono all’indietro con Un contatore asincrono all’indietro con modulo pieno ( ), rappresentato nella sottostante figura (a) e in figura (b) con il suo simbolo

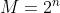
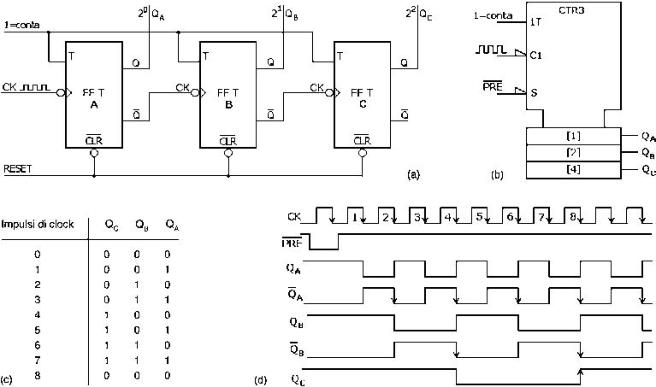
Contatore asincrono, all’indietro, modulo 8: (a) realizzazione con flip-flop T di tipo NET, (b) simbolo logico, (c) tabella degli stati, (d) diagramma dei tempi

logico o, può essere ottenuto con una piccola modifica dell’up counter sopra mostrato: il segnale di clock ai flip-flop successivi deve essere dato da e non da Q; le uscite invece restano invariate, cioè sono date sempre dalle linee dirette Q. Il down counter deve essere forzato nella sua configurazione iniziale 111 e per fare ciò è necessario disporre di un ingresso di set (chiamato anche preset). In corrispondenza del fronte di discesa del primo impulso di clock il flip-flop A commuta portandosi a livello basso; i flip-flop successivi invece restano bloccati poiché il loro cambiamento di stato si può verificare solo sul fronte negativo di Q da cui sono comandati. Pertanto la nuova configurazione del contatore è 110. Il conteggio degli impulsi, seguendo la numerazione binaria, evolve fino allo stato finale 000; l’ottavo impulso di clock riporta il circuito nella configurazione iniziale (111) ed il conteggio può ripartire dall’origine della sequenza. La soprastante figura (d) riporta il diagramma dei tempi e la tabella degli stati è mostrata in figura ( c). Analogamente al contatore in avanti anche il down counter può essere costruito con flip-flop T positive edge triggered; in questo caso sono i segnali Q a comandare i flipflop successivi. Le uscite restano ancora una vota invariate.

Contatore asincrono bidirezionale

Un contatore asincrono binario si definisce avanti/indietro o bidirezionale se è in grado di contare sia in avanti sia all’indietro. Dai contatori costruiti con flip-flop T che commutano sul fronte di discesa, si deduce che per ottenere un conteggio in avanti è necessario comandare i flip-flop successivi con le linee Q, mentre per contare all’indietro il segnale di comando deve pervenire da . Se invece si utilizzano invece flip-flop T che commutano sul fronte di salita il conteggio in avanti si ottiene con i segnali , mentre con le uscite Q si realizza un contatore all’indietro. L’organizzazione circuitale di un contatore bidirezionale è funzione sia del tipo di flip-flop positive o negative edge triggered, sia delle uscite Q e utilizzate come segnali di comando. Nella sottostante fogura (a) è riprodotto lo schema logico di un contatore avanti/indietro (up/down) con flip-flop T positive edge, triggered mentre in figura (b) i flip-flop utilizzati commutano sul fronte negativo.

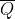
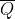
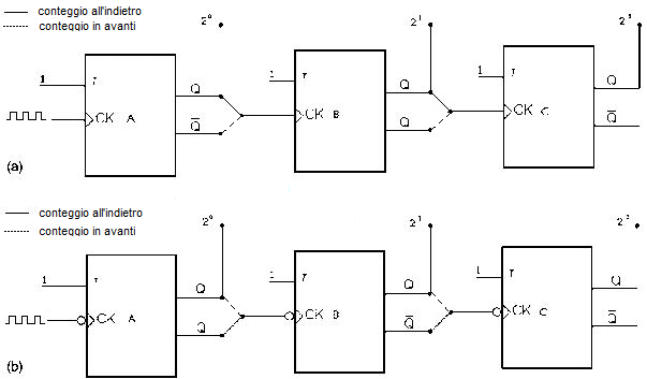
Si può inserire una rete combinatoria (MUX) per smistare uno dei due segnali (Q o ) nel clock del flip-flop successivo, come mostrato nella seguente figura.

Contatore bidirezionale (up/down): (a) realizzato con flip-flop T di tipo PET, (b) realizzato con flip-flop T di tipo NET

Contatore asincrono, binario, bidirezionale

Contatori asincroni con modulo Spesso nella tecnica delle misure e in genere in tutti i sistemi digitali sono necessari contatori il cui ciclo deve essere inferiore alla capacita massima di conteggio. Il modulo risulta così minore di ; si tratta, in definitiva, di contatori caratterizzati da una sequenza di conteggio troncata. Un tipico esempio è quello del contatore decadico (M = 10), costruito a partire da un asincrono a quattro bit (M = 16) che conta da 0 a 9, salta le configurazioni da 10 a 15 e torna a 0 (vedi tabella a lato).

Tabella degli stati di un contatore decadico.

Impulsi di clock

Si possono costruire contatori con un qualsiasi modulo rispettando tuttavia la condizione che tale vincolo serve anche a individuare il numero di flip-flop strettamente indispensabili. Se ad esempio si desidera un contatore modulo 5 essendo sono necessari tre flip-flop. Esempio Si vuole realizzare un contatore asincrono up con modulo 6 a partire dall’asincrono up con modulo pieno a 3 bit. Nella sottostante tabella a lato, sono mostrati i relativi stati. La trasformazione di un contatore in uno a sequenza troncata (come in figura (a)) si può realizzare con una porta NAND, la cui uscita attiva la linea di clear quando si verifica la prima configurazione non desiderata, che nel nostro caso è Qc=1, Qb=1, QA=0. In realtà gli ingressi della porta NAND possono essere limitati a QC e QB dato che essi non assumono mai contemporaneamente il livello 1 nella sequenza degli stati utili. Dal soprastante diagramma dei tempi, si nota che lo stato QC QB QA = 110 persiste sulle uscite del contatore per un certo tempo (dovuto sia al ritardo di propagazione della porta NAND sia al tempo di reset dei flip-flop). Tale ritardo nell’azzeramento causa un impulso indesiderato (glitch) che costituisce fonte di disturbo se le uscite del contatore devono pilotare un altro circuito digitale. In pratica potrebbe verificarsi un inconveniente in un contatore asincrono di questo tipo. Il problema è dovuto ai differenti tempi di commutazione dei flip-flop. Infatti se un flip-flop si azzera in un tempo inferiore rispetto agli altri, le uscite del contatore, non attivando più la porta NAND, disabilitano la linea di clear con il risultato che il contatore riparte da una configurazione casuale. L’inconveniente può essere superato con l’introduzione di un latch come indicato nella sottostante configurazione. Il latch è inizialmente settato (Q = 1) e vi rimane fintanto che la AND ha l’uscita a 0.

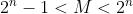
Tabella degli stati di un contatore M = 6.

Impulsi di clock

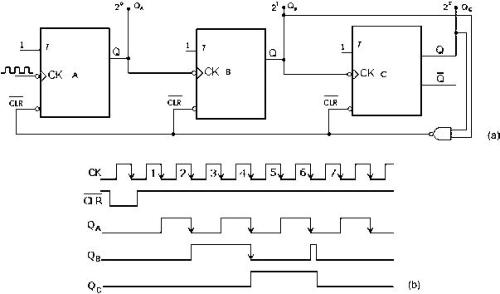
Contatore asincrono, in avanti, modulo 6: (a) realizzazione con flip-flop T di tipo NET, (b) diagramma dei tempi.

Circuito di reset del contatore realizzato con un latch SR.

ché la AND ha l’uscita a 0. S è collegato al CK quindi in ingresso si alternano due configurazioni: SR = 00 che blocca il latch e SR = 10 che lo setta. Quando la AND viene attivata dalle uscite del contatore, SR = 01 porta l’uscita Q a 0: la linea di clear viene attivata. Se un flip-flop del contatore si resetta in un tempo inferiore rispetto agli altri, l’uscita della AND si porta a 0 e il latch rimane bloccato con l’uscita Q = 0 garantendo il reset di tutto il contatore. L’arrivo di un impulso di clock setta nuovamente il latch disattivando la linea di clear.

Contatore asincrono up BCD Un contatore con sequenza troncata di particolare interesse perché consente il conteggio delle 10 cifre decimali (da 0 a 9) è il contatore decadico. Sulle quattro linee di uscita sono rappresentate nel codice BCD le 10 cifre decimali. Il contatore asincrono BCD in avanti si può ottenere dal contatore asincrono modulo 16 impedendo che si verifichino le configurazioni da 10 a 15. L’operazione di reset deve avvenire nel passaggio dallo stato 1001 allo stato 1010. Se i flip-flop utilizzati hanno un reset attivo a livello basso, con una porta NAND (vedi la sottostante figura), comandata dai segnali QB e QD, si può resettare il contatore. È superfluo utilizzare anche le uscite QA e QC per pilotare la porta NAND poiché Qb e Qd assumono contemporaneamente il livello 1 alla prima configurazione illegale. L’inconveniente maggiore presentato da questo circuito è costituito dal fatto che la configurazione 10 deve apparire sulle uscite (figura (b)) perché intervenga la porta NAND ad azzerare i flip-flop. Questo tipo di reset è fonte di notevoli disturbi e pertanto nei contatori integrati MSI sono adottate soluzioni circuitali più complesse per evitare l’inconveniente.

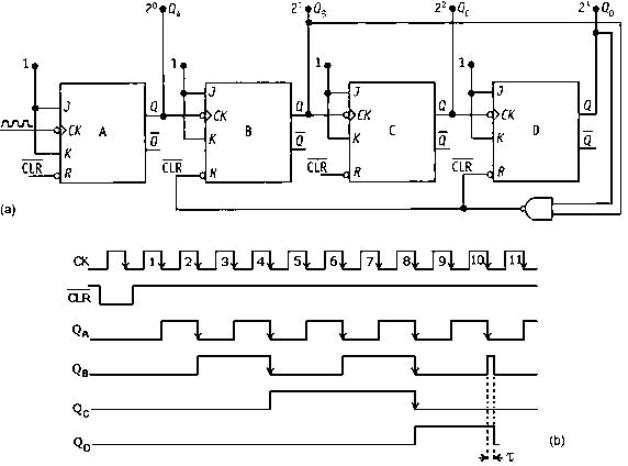
Contatore asincrono down BCD Si può realizzare un contatore asincrono BCD all’indietro a partire da un down counter binario a quattro bit. È necessario però disporre di un comando di set per inizializzare il circuito sulla cifra decimale 9 prima dell’inizio del conteggio evidenziato nella sottostante figura. Contatore asincrono, all’indietro, di tipo BCD La porta NAND serve a resettare i flip-flop C e B per portare il contatore nella configura- -zione 1001. È possibile limitare gli ingressi della porta NAND ai soli segnali QD e QC dato che essi non assumono mai contemporaneamente il livello alto tra le configurazioni utili.

Limiti di funzionamento dei contatori asincroni Per poter lavorare correttamente con un contatore asincrono è necessario tener presente che in alcuni casi si può incorrere in errori nel rilevamento del dato ed in altri casi in errori in fase di decodifica dei risultati del conteggio.

Limiti di frequenza del segnale d’ingresso Nel tracciamento dei diagrammi dei tempi dei contatori asincroni è necessario tener conto di due fattori importanti: • ogni flip-flop non può commutare istantaneamente in corrispondenza del fronte di salita o di discesa dell’impulso di comando poiché necessita di un certo tempo, chiamato ritardo di propagazione (tPD, Propagation Delay), affinché avvenga effettivamente la variazione di livello dell’uscita; • il modo stesso di funzionamento del contatore è definito asincrono perché gli stadi successivi ricevono il segnale di commutazione da quello precedente.

Si consideri il diagramma dei tempi sotto evedenziato, di un contatore asincrono up con M = 16 tenendo conto dei ritardi di propagazione dei flip-flop. A partire dal fronte negativo del primo impulso di clock il flip-flop A passa da 0 a 1 dopo un tempo di 25 ns (valore tipico). Tutti gli stadi successivi non devono commutare, pertanto il ritardo totale rimane di 25 ns. Il problema dei ritardi diventa più gravoso quando, passando da una configurazione ad un’altra, devono commutare più o tutti gli stadi. Si esamini il comportamento del contatore quando deve passare dalla posizione 1111 a 0000. Dal fronte negativo del sedicesimo impulso il flip-flop A commuta con un ritardo di 25 ns, quindi con tale ritardo il fronte di discesa viene inviato al secondo stadio che a sua volta, dopo 25 ns, si porta a 0. Così il processo di accumulo dei ritardi si propaga fino all’ultimo stadio che cambia livello dopo un tempo pari a 100 ns; ovviamente nell’ipotesi che tutti i flip-flop abbiano uguale ritardo di propagazione. Nell’intervallo di tempo che intercorre tra il fronte di discesa del sedicesimo impulso e la commutazione dell’ultimo flip-flop non devono giungere altri fronti negativi del segnale di clock poiché ciò comporterebbe una nuova commutazione del primo stadio e quindi una errata interpretazione dei risultati. Tutto ciò costituisce un limite al periodo del clock che deve essere:

Diagramma dei tempi di un contatore asincrono, in avanti, modulo 16, con posti in evidenza i ritardi di propagazione

mentre per la frequenza del clock si può scrivere che

Questa è senz’altro la condizione più restrittiva che si possa imporre in quanto corrispo- -nde alla situazione più gravosa in cui lavora il circuito. Nel caso ipotizzato il limite della frequenza del clock è di 10 MHz. Se si pone tale condizione come limite alla frequenza del segnale di clock è possibile effettuare l’operazione di lettura senza incorrere in errori. Se invece si intende eseguire la lettura solo alla fine del conteggio, la condizione imposta non ha più validità, essendo la massima frequenza del segnale d’ingresso vincolata solo al corretto funzionamento del primo stadio e quindi al valore massimo della frequenza del primo flip-flop. Il limite della frequenza del clock sale a 20 MHz.

Errori in fase di decodifica Un altro problema causato dai ritardi di propagazione dei flip-flop è costituito dalla generazione dei glitches in fase di decodifica. Si consideri il diagramma reale dei tempi del decodificatore di un contatore con M = 4 riportato nella figura a destra. A causa del ritardo di propagazione, dopo il secondo fronte negativo del clock, si verifica uno stato illegale QB = QA = 0 e aleatorio, che origina un impulso spurio (glitch) sull’uscita del decodificatore. Dall’osservazione del diagramma dei tempi si nota che, se il modulo del contatore è M, in genere il numero dei glitches è M/2. Poiché l’eliminazione di questi impulsi è un’operazione estre- -mamente complessa, conviene impedire la nascita di questi glitches. Una delle soluzioni più semplici è la tecnica dello strobing (mostrata a lato) che consiste nell’attivare le porte AND del decodificatore per un tempo breve, ma abbastanza lontano dal fronte di commutazione del clock.

Rete di decodifica di un contatore con ingresso di strobe

Contatori sincroni I contatori sincroni sono caratterizzati dal funzionamento simultaneo di tutti i flip-flop, come mostrato nella sottostante figura. Possono essere costruiti con flip-flop T, JK e SR con qualunque tipo di temporizzazione, anche se i master-slave danno una maggiore affidabilità. Poiché in questi contatori il segnale di clock viene inviato a tutti i flip-flop contempora- -neamente, è necessaria una rete combinatoria che dia agli ingressi dati le eccitazioni opportune in modo tale da far commutare i flip-flop secondo la sequenza di conteggio. Ogni contatore sincrono, a sequenza piena ( ) o troncata ( ), richiede una specifica progettazione che tenga conto di vari fattori quali il modulo, la direzione di conteggio e il tipo di flip-flop utilizzati. Tale progettazione si articola in varie fasi che possono essere così riassunte: • scelta del modulo e direzione di conteggio, esprimibili graficamente con un diagramma di flusso; • scelta del tipo di flip-flop da utilizzare; • costruzione della tabella di eccitazione dei flip-flop; • funzioni e minimizzazione con le mappe di Karnaugh; • realizzazione della rete di eccitazione sulla base delle funzioni minimizzate. Si possono costruire contatori sincroni in avanti, all’indietro e bidirezionali.

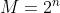
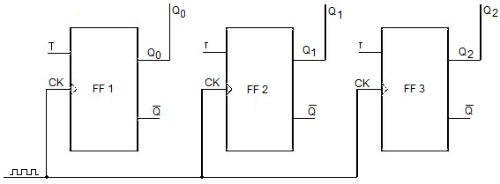
Contatori sincroni con I contatori sincroni se hanno un modulo si definiscono a sequenza piena o modulo pieno. Come esempio si supponga di voler costruire un contatore sincrono up con M = 8. Si seguono le fasi di progetto esposte nel paragrafo precedente. • Prima fase: diagramma di flusso. Il funzionamento del contatore è schematizzabile graficamente con un diagramma di flusso che rappresenta la sequenza di conteggio e il modulo. In un cerchietto si racchiude lo stato del circuito mentre con una freccia si indica il passaggio dallo stato precedente a quello successivo in corrispondenza di ogni impulso di clock. Nella sottostante figura è disegnato il diagramma di flusso di un contatore con modulo 8. • Seconda fase: scelta del tipo di flip-flop. Con M = 8 sono necessari tre flip-flop, per semplicità si scelgono di tipo T NET. • Terza fase: tabella di eccitazione. Si costruisce la tabella di eccitazione dei flip-flop ricordando che il tipo T commuta solo quando T = 1. Se il contatore si trova nello stato di partenza 000 e deve commutare nello stato futuro 001, gli ingressi devono essere eccitati con TA=1 e TB=TC= 0 poiché solo il flip-flop A deve commutare (figura b). Analogamente se lo stato presente è 001 e lo stato successivo è 010, gli ingressi T devono essere quelli indicati nella figura c. Le uscite dei flip-flop A e B cambiano livello quindi TB e TA devono essere uguale a 1 mentre il flipflop C resta bloccato e pertanto TC = 0. La tabella di eccitazione può essere completata procedendo in modo analogo per tutte le altre configurazioni (figura d). • Quarta fase: mappe di Karnaugh. La tabella ottenuta con questo metodo può essere vista come una function table con variabili indipendenti QC QB QA e dipendenti TC TB TA, pertanto le equazioni funzionali dedotte dalla tabella e minimizzate con le mappe di Karnaugh (figura e) sono: • Quinta fase: realizzazione della rete di eccitazione. Ottenute le funzioni minimizzate si passa alla realizzazione del circuito che è riportato in figura f.

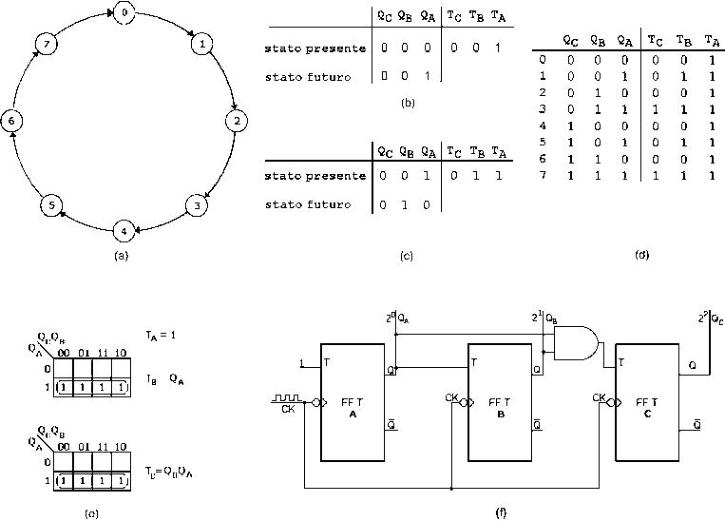
Contatore sincrono, in avanti, modulo 8: (a) diagramma di flusso, (b) tabella di eccitazione al primo impulso di clock, (c) tabella di eccitazione al secondo impulso di clock, (d) tabella di eccitazione completa del contatore, (e) mappe di Karnaugh, (f) realizzazione circuitale

Contatore con riporto serie e parallelo La rete di eccitazione del contatore può essere realizzata in due modi differenti dando luogo a due tipi di contatore: uno con riporto serie, l’altro con riporto parallelo. Se le funzioni T sono scritte in relazione esclusiva dei Q, la rete combinatoria è costituita da porte AND con un numero di ingressi via via crescente. Il riporto è di tipo parallelo. Se le funzioni T sono scritte in relazione ai segnali Q e ai T dei flip-flop precedenti, la rete combinatoria è costituita da porte AND con due ingressi qualunque sia la lunghezza del contatore. In questo caso il riporto è di tipo serie. Il contatore con riporto serie ha il vantaggio di avere porte AND a due ingressi ma presenta lo svantaggio di commutare in un tempo maggiore poiché ogni porta AND riceve il segnale d’ingresso da una porta AND precedente, accumulando così i ritardi di propagazione. Esempio Si vuole realizzare un contatore sincrono in avanti con M = 16. Sono necessari quattro flip-flop, ad esempio di tipo T, da collegare in modo sincrono. Conoscendo il modulo e la direzione del conteggio, si traccia il diagramma di flusso riportato nella sottostante figura (a). Dalla tabella di eccitazione (figura b) si ricavano le equazioni funzionali rese in forma minima con le mappe di Karnaugh di figura c. Le funzioni che si ottengono sono le seguenti:

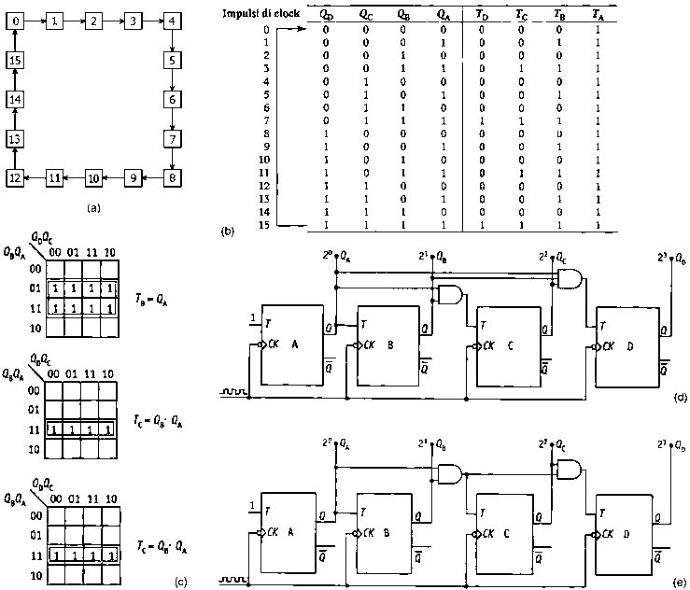
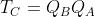
Da queste funzioni si ricava un contatore che si definisce sincrono in avanti con riporto parallelo (figura d), perché le porte AND, il cui numero di ingressi è crescente, lavorano in parallelo tra di loro. Le funzioni semplificate possono essere scritte anche nella seguente forma:

Il circuito (figura e) dedotto da queste funzioni presenta porte AND con un numero di ingressi costanti che lavorano in serie tra di loro, infatti l’uscita di una porta AND costituisce un ingresso per quella successiva. Questo tipo di contatore ha riporto serie.

Contatore sincrono all’indietro con Per progettare un contatore sincrono all’indietro con modulo pieno è necessario seguire la stessa procedura adottata per il contatore in avanti. Contatore sincrono, all’indietro, modulo 8: (a) diagramma di flusso, (b) tabella di eccitazione al primo impulso di clock, (c) tabella di eccitazione al secondo impulso di clock, (d) tabella di eccitazione completa del contatore, (e) mappe di Karnaugh, (f) realizzazione circuitale • Prima fase: diagramma di flusso. Si disegna il diagramma di flusso (figura a) del contatore, ad esempio con M = 8, quindi con configurazione iniziale 111. • Seconda fase: scelta del tipo di flip-flop. Si valuta il numero di flip-flop necessari, nel caso in esame n = 3, e si sceglie il tipo di flip-flop necessariamente temporizzato. Per esempio flip-flop T NET. • Terza fase: tabella di eccitazione. Se il circuito si trova nello stato 111, lo stato futuro è 110. Dunque deve commutare solo flip-flop A, quindi TA = 1 mentre TB = TC = 0, come indicato in figura (b). Al secondo impulso di clock, quando lo stato presente è 110, le uscite assumeranno la configurazione 101, di conseguenza dovranno commutare i flip-flop A e B (figura c). • Quarta fase: mappe di Karnaugh. Dopo aver costruito così tutta la tabella di eccitazione (figura d) si procede alla semplificazione delle funzioni con le mappe di Karnaugh, riportate in figra (e). Le funzioni semplificate risultano le seguenti:

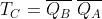
• Quinta fase: realizzazione della rete di eccitazione. Tenendo presente le funzioni ottenute, si disegna lo schema circuitale del contatore (figura (f)). Dal confronto tra i contatori in avanti e all’indietro si rileva che la differenza tra i due consiste semplicemente nello scambio dei segnali Q e Q per il comando degli ingressi T.

Contatore sincrono down con riporto serie e parallelo Anche il contatore all’indietro può essere realizzato con riporto serie e parallelo. Schema circuitale del contatore sincrono, all’indietro, a 4 bit, con riporto serie. Il soprastante circuito è un contatore sincrono a 4 bit con riporto serie poiché ogni porta AND riceve il segnale d’ingresso dalla AND precedente. Le funzioni di eccitazione possono essere scritte anche nella seguente forma

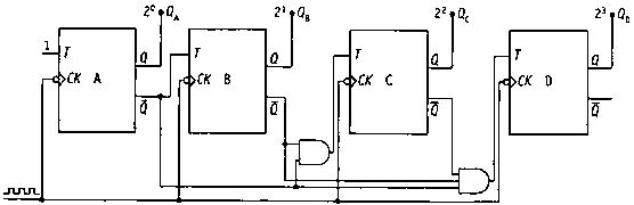
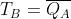
Schema circuitale del contatore sincrono, all’indietro, a 4 bit, con riporto parallelo

Il contatore sopra raffigurato, ottenuto con queste funzioni è a riporto parallelo, infatti le porte AND sono eccitate in parallelo. La differenza tra i due tipi di contatore riguarda il tempo di commutazione che è più breve in quello parallelo.

Realizzazione di un contatore bidirezionale tramite un multiplexer

Contatore sincrono bidirezionale con Il contatore sincrono con modulo può contare in modo bidirezionale (up/down) utilizzando una rete di selezione (multiplexer) per smistare sugli ingressi T i segnali Q e Nella sottostante figura è riportato lo schema.

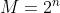
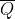
Contatori sincroni con I contatori sincroni con modulo sono caratterizzati da una sequenza troncata. Tra tutti i contatori con sequenza troncata i più importanti sono senz’altro i decadici (a modulo 10), chiamati anche BCD o decimali.

Contatore sincrono BCD in avanti Per la progettazione dei contatori con sequenza troncata si utilizza la stessa procedura dei contatori con sequenza piena. • Prima fase: diagramma di flusso. Si traccia il diagramma di flusso del contatore (rappresentato un figura a). Le configurazioni da 10 a 15, che non fanno parte della sequenza di conteggio, possono essere valutate come condizioni di indifferenza

• Seconda fase: scelta del tipo di flip-flop. Il flip-flop scelto è il tipo JK master-slave, di cui è necessario conoscere la tabella delle transizioni (fig. 16.91b) che serve a stabilire le eccitazioni da dare agli ingressi J e K perché avvenga la transizione dallo stato presente a quello futuro. Se per esempio il flip-flop si trova nello stato 0 (uscita Q = 0) e deve portarsi nello stato futuro che è ancora 0, si possono eccitare gli ingressi J e K con J = 0 e K = 0 ovvero con J = 0 e K = 1, infatti entrambe le coppie di ingressi producono lo stesso risultato: il flip-flop resta bloccato nello stato 0. Nella tabella queste due possibilità di eccitazioni sono sintetizzate con un’unica configurazione J = 0 e K = X. • Terza fase: tabella di eccitazione. Tenuto conto della tabella delle transizioni del flip-flop JK si può scrivere la tabella di eccitazione del contatore sincrono BCD, riportata in figura c. • Quarta fase: mappe di Karnaugh. Con le mappe di Karnaugh (figura d) si semplificano le funzioni per ridurle in forma minima. • Quinta fase: realizzazione della rete di eccitazione. Si disegna la rete combinatoria di eccitazione a partire dalle funzioni semplificate ottenute (vedi figura e).

Contatore sincrono, in avanti, di tipo BCD: (a) diagramma di flusso, (b) tabella delle transizioni del flip-flop JK, (c) tabella di eccitazione del contatore, (d) mappe di Karnaugh, (e) realizzazione circuitale

Stati di blocco Un problema che si presenta spesso nei contatori sincroni con sequenza troncata è il verificarsi, per effetto di un disturbo oppure al momento dell’accensione, di una delle configurazioni illegali. È necessario quindi assicurarsi che il contatore rientri nel regolare ciclo di conteggio poiché vi è la possibilità che il circuito resti bloccato, se privo di un ingresso di reset o di preset. Se, ad ogni impulso di clock, il contatore passa da uno stato illegale ad un altro senza rientrare nel regolare ciclo di conteggio, si dice che il circuito è in uno stato di blocco. La verifica degli eventuali stati di blocco si esegue ipotizzando uno stato illegale del contatore e calcolando con le funzioni i nuovi ingressi di eccitazione dei flip-flop. Esempio Si supponga di voler verificare l’esistenza di eventuali stati di blocco nel contatore sincrono BCD in avanti del paragrafo precedente. Se lo stato presente del contatore, QD=1, QC=0, QB=1, QA=0, è illegale, inserendo tali valori nelle funzioni (figura d), si ricavano i nuovi ingressi J e K:

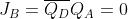
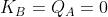
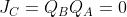
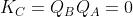
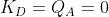
Con queste eccitazioni il nuovo stato sarà il seguente: • flip-flop A commuta: QA =1; • flip-flop B bloccato: QB = 1; • flip-flop C bloccato: QC = 0; • flip-flop D bloccato: QD = 1. Si deduce quindi che dallo stato 1010 il circuito si porta a 1011. Si può costruire così la tabella (b) a lato relativa a questi stati illegali e completare il diagramma di flusso mostrato in figura (a), tenendo conto anche di queste configurazioni. Dalla tabella e dal diagramma di flusso (a) si deduce che non vi sono stati di blocco. Per evitare che questo inconveniente possa verificarsi, si può, in sede di progetto, pro- -grammare il rientro da uno stato illegale in un qualsiasi punto della regolare sequenza di conteggio.

Stati di blocco nel contatore sincrono, in avanti, di tipo BCD: (a) diagramma di flusso completo, (b) tabella degli stati illegali

Limiti di frequenza del segnale d’ingresso I contatori sincroni, abbastanza veloci data la simultaneità di funzionamento dei flip-flop, necessitano di una rete di eccitazione che genera inevitabilmente un aumento dei tempi di funzionamento. Ad esempio il contatore sincrono up con M = 16 con riporto parallelo sopra mostrato presenta un ritardo di commutazione pari alla somma del ritardo di propagazione tPD AND della porta AND e del ritardo di propagazione tPD FF del flip-flop, nell’ipotesi che siano tutti uguali tra loro i e del ritardo di propagazione del flip-flop, nell’ipotesi che siano tutti uguali tra loro i delle AND e i dei flip-flop. Il periodo del clock risulta:

Contatore sincrono, in avanti, modulo 16, con riporto parallelo.

Il contatore sincrono con riporto serie mostrato sotto, necessita di un tempo di commuta- -zione maggiore rispetto a quello parallelo poiché i segnali logici, propagandosi attraverso la serie delle porte AND, impongono una ulteriore limitazione alla velocità di funzionamento.

Contatore sincrono, in avanti, modulo 16, con riporto serie

Il tempo di ritardo complessivo del contatore sincrono con M = 16 con riporto serie sarà dato da:

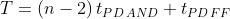
La frequenza del segnale di clock deve quindi rispettare la seguente condizione:

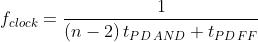
Errori in fase di decodifica La rete di decodifica di un contatore sincrono non presenta diversità da quella di un contatore asincrono. Errori in fase di decodifica, possibili anche in un contatore sincrono, sono dovuti: • ai tempi non nulli di salita e di discesa del segnale di uscita; • alle inevitabili differenze di questi tempi; • alle differenze del ritardo di propagazione tra i vari flipflop. La durata di questi errori, peraltro estremamente breve, non dipende dal numero degli stadi di cui il contatore è costituito a differenza di quanto avviene invece negli asincroni. La simultaneità di funzionamento dei flip-flop riduce notevolmente la probabilità di glitches. Gli errori di decodifica sono indipendenti dalla frequenza di funzionamento del circuito.

Confronto tra contatori sincroni e asincroni I contatori asincroni presentano rispetto a quelli sincroni i seguenti vantaggi: • sono decisamente più veloci, se si intende effettuare la lettura alla fine del conteggio oppure se devono essere usati come divisori di frequenza; • sono più semplici costruttivamente; • sono più economici • hanno un minore assorbimento di potenza. Limiti dei contatori asincroni: • a causa della commutazione in sequenza dei flip-flop per tutto il tempo di assestamento del circuito, vengono generate sulle uscite configurazioni illegali; • in conseguenza del difetto precedente, in fase di decodifica sono presenti sicuramente dei glitches, estremamente difficili da eliminare; • il numero e la durata degli errori di decodifica aumentano all’aumentare del numero degli stadi.

Un contatore BCD (sincrono o asincrono) conta da 0 a 9; per poter contare nel sistema decimale numeri a più cifre (unità, decine, centinaia) è necessario poter disporre di più contatori BCD collegati tra di loro: Il segnale di clock tra una decade inferiore e quella superiore garantisce la progressione del conteggio, infatti, supponendo inizialmente tutte le uscite a zero, quando il BCD di peso inferiore (ad esempio delle unità) passa dal 9 allo 0, il segnale QD si porta da 1 a 0 fornendo così l’impulso di clock al BCD superiore (delle decine). Il conteggio evolve dalle unità alle decine, dalle decine alle centinaia e così via. La visualizzazione del risultato si effettua facilmente inviando i segnali di ciascun BCD ad un decodificatore BCD/segmenti che pilota un display a 7 segmenti.

Contatore a più decadi

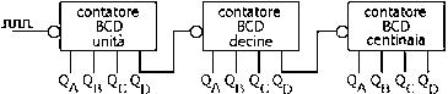
Contatore BCD a 3 decadi.

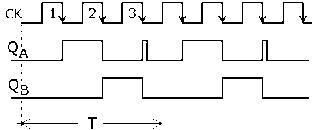
Contatori come divisori di frequenza Un contatore, sincrono o asincrono, può essere utilizzato per generare segnali aventi una frequenza inferiore a quella del segnale di clock. Il contatore funge anche da divisore o riduttore di frequenza. Dal diagramma dei tempi di figura (a) di un contatore (sincrono o asincrono) in avanti con M = 16 si osserva che: • l’uscita QA ha una frequenza pari a 1/2 del segnale di clock; • l’uscita QB ha una frequenza uguale a 1/2 di QA e a 1/4 del clock; • l’uscita QC ha una frequenza uguale a 1/2 di QB e a 1/8 del clock; • l’uscita QD ha una frequenza uguale a 1/2 di QC e a 1/16 del clock.

(a) Diagramma dei tempi di un contatore in avanti, a 4 bit, utilizzato come divisore 16:1 e (b) diagramma dei tempi di un contatore all’indietro, a 4 bit, utilizzato come divisore 16:1

Anche i contatori all’indietro si comportano come divisori di frequenza con la differenza però che i livelli alti e quelli bassi sono scambiati tra di loro rispetto al contatore in avanti mostrato in figura (b). Utilizzando contatori a sequenza troncata si possono ottenere rapporti, segnale di uscita/segnale di clock, non necessariamente potenze di 2. Nella figura a lato è riportato come esempio il diagramma dei tempi di un contatore asincrono M = 3, come divisore 3:1. Il segnale di uscita ha un duty cycle (rapporto tra durata del livello alto e durata dell’intero periodo) diverso dal 50% e questo in molte applicazioni è inaccettabile. In alcuni casi il problema è facilmente risolvibile

Contatori integrati MSI TTL e CMOS Per progettare un contatore, secondo i metodi tradizionali di progetto, esaminati nei paragrafi precedenti, è necessario partire dai flip-flop e dalle porte logiche. Questo tipo di procedimento, piuttosto lungo e laborioso, si rivela utile solo se il contatore da progettare è di basso modulo ed in ogni caso fa aumentare la probabilità di introdurre impulsi indesiderati e stati non consentiti. In tutti gli altri casi è preferibile impiegare contatori integrati MSI, TTL o CMOS, di cui in commercio esiste una grande varietà in grado di soddisfare le più diverse esigenze. Non bisogna inoltre sottovalutare che gli integrati MSI sono molto spesso economicamente più vantaggiosi. L’integrato CMOS 4029 è un contatore avanti-indietro presettabile che conta in modo binario o decadico in funzione del livello di tensione applicato all’ingresso BIN/DEC, pin 9. L’integrato 74HC190 è un contatore sincrono decadico, BCD, bidirezionale con possibilità di caricamento dati asincrono, ovvero tramite il comando di preset.

Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara

Home