



La vita è ciò che ti accade quando sei tutto intento a fare altri piani.
ELETTRONICA DIGITALE
… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!
MAPPA DI KARNOUGH


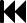

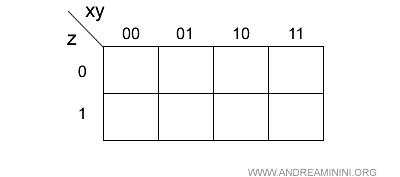
Definizioni
La mappa di Karnaugh è un metodo di rappresentazione esatta
di sintesi di reti combinatorie a uno o più livelli.
Una tale mappa costituisce una rappresentazione visiva di una
funzione booleana in grado di mettere in evidenza le coppie di
mintermini o di maxtermini a distanza di Hamming unitaria
(ovvero di termini che differiscono per una sola variabile binaria
(o booleana)).
Poiché derivano da una meno intuitiva visione delle funzioni
booleane in spazi con
numero delle variabili della fun-


-zione, le mappe di Karnaugh risultano applicabili efficacemente solo a funzioni con al più
5 - 6 variabili.
Una mappa di Karnaugh è un metodo grafico che ha come obiettivo quello di ridurre la com-
-plessità delle funzioni booleane espresse in forme canoniche.
Essa si costruisce a partire dalla tabella della verità di una funzione booleana, nel processo
di sintesi di una rete combinatoria.
Le mappe di Karnaugh permettono di costruire semplicemente la forma minima di una
funzione come somma di prodotti logici (forma disgiuntiva) o come prodotto di somme
logiche (forma congiuntiva) e quindi semplificazioni della funzione booleana spesso più
immediate di quelle ottenibili con modifiche algebriche.

Come trovare la mappa di Karnaugh
Il metodo funziona soltanto se l'espressione è in forma normale disgiuntiva ( DNF ).
Nota.
Per ogni funzione logica esiste sempre un'espressione booleana in forma normale
disgiuntiva ed è unica. Inoltre, le clausole devono essere composte dagli stessi
letterali.

Esempio
Questa espressione booleana è composta da tre clausole.
La terza clausola non ha il letterale z.
Per risolvere il problema, la trasformo in una somma di clausole con la z attiva e negata.



Nota.
Questa espressione booleana equivale a un circuito logico con quattro porte
AND, una porta OR e quattro porte NOT. Complessivamente, il circuito è composto
da 9 porte.

La tavola di verità dell'espressione è
1] Costruire la mappa
Scelgo due gruppi di letterali dell'espressione.
Ad esempio xy e z.
Poi costruisco una tabella mettendo le xy sulle colonne e la z sulle righe.
Nelle righe e nelle colonne indico le combinazioni di valori (0,1) che i letterali z e xy
possono assumere.
2] Individuare le celle della mappa a cui corrispondono le clausole dell'espressione
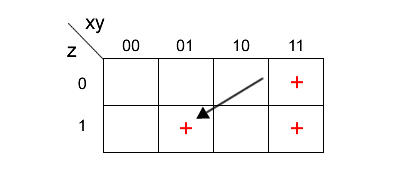
Prima clausola
La prima clausola dell'espressione è
Equivale a xy=11 * z=1.
Questa clausola corrisponde alla cella in cui si incrociano l'ultima colonna
(xy=11) e la seconda riga (z=1) della mappa.


Seconda clausola
La seconda clausola dell'espressione è
Equivale a xy = 11 e z=0.
Questa clausola corrisponde alla cella in cui si incrociano l'ultima colonna (xy=11) e
la prima riga (z=0) della mappa.


Terza clausola
La terza clausola dell'espressione è
Equivale a xy = 01 e z=1.
Questa clausola corrisponde alla cella in cui si incrociano la seconda colonna (xy=01)
e la seconda riga (z=0) della mappa.
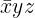
Quarta clausola
La quarta clausola dell'espressione è
Equivale a xy = 01 e z=0.
Questa clausola corrisponde alla cella in cui si incrociano la seconda colonna (xy=01) e
la prima riga (z=0) della mappa.

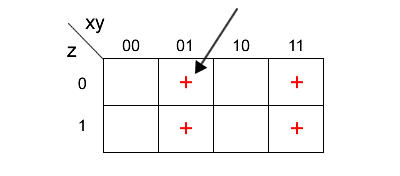
3] Raggruppare le celle confinanti in gruppi di 2, 4 o 8 elementi
Una volta costruita la mappa di Karnaugh, posso raggruppare i simboli per multipli di 2.
Ogni gruppo deve essere composto da 2,4,8 simboli vicini tra loro.
I gruppi possono anche sovrapporsi parzialmente.
Nota. Le pareti della mappa di Karnaugh confinano con la parete opposta.
In questo caso, nella mappa ci sono due gruppi da 2.

4] Trasformare i gruppi in congiuzioni di letterali
Prendo ciascun gruppo e lo trasformo in una congiunzione, eliminando i letterali che
assumono contemporaneamente i valori 0 e 1.
Primo gruppo
Nel primo gruppo xy assume il valore 01.
Elimino, invece, il letterale z perché ha sia il valore 0 che 1.
Il risultato finale è


Secondo gruppo
Nel primo gruppo xy assume il valore 11.
Elimino, invece, il letterale z perché ha sia il valore 0 che 1.
Il risultato finale è


5] Sommare le congiunzioni di letterali
Sommo tra loro le congiunzioni appena trovate e ottengo l'espressione booleana in forma
ridotta della funzione booleana.
Il nuovo circuito logico è composto soltanto da due porte AND, una porta OR e una
porta NOT. Complessivamente, il circuito ha 4 porte.


La tavola di verità dell'espressione è sempre la stessa.
Anche se non c'è più la lettera z, il valore 1 è abbinato alle stesse combinazioni x, y
della precedente

Nota. L'espressione è sicuramente migliore rispetto all'espressione iniziale.
Tuttavia, non è ancora ottimale. Come si può vedere, nelle due clausole il letterale x
appare sia in forma diretta che negata.
Una semplice regola di semplificazione consente di eliminare la x in entrambe le clausole.
L'espressione si riduce a
Un'altra legge dell'algebra booleana mi permette di ridurre ulteriormente l'espressione in
Perché la mappa di Karnaugh non l'ha trovata? Perché il risultato dipende anche dalla
scelta dei gruppi di letterali e dall'ordine delle colonne nella mappa.

Come migliorare la mappa di Karnaugh
La riduzione di un'espressione booleana tramite la mappa di Karnaugh dipende dalla scelta
dei gruppi e dall'ordine delle colonne.
Ad esempio, riprendo la precedente mappa scambiando la posizione della quarta e della
terza colonna.
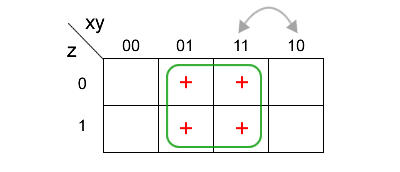
In questo modo creare un gruppo di quattro celle.
Il nuovo raggruppamento permette di semplificare ulteriormente il risultato finale.
Sia la z che la x appaiono con il segno zero e con il segno meno.
Quindi, posso eliminarle.

L'espressione finale è
Ovviamente l'espressione non può essere ulteriormente ridotta.
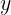


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





