



La vita è ciò che ti accade quando sei tutto intento a fare altri piani.
ELETTRONICA DIGITALE
… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!
ALGEBRA BOOLEANA




L'algebra booleana è un sistema di logica matematica
a due stati, dove le variabili ( dette variabili booleane )
possono assumere solo due stati: vero (1) o falso (0).
Le leggi dell'algebra booleana sono strettamente vicini a quelle
della logica e all'insiemistica.
La storia dell'algebra booleana
L'algebra booleana venne ideata dal matematico inglese George
Boole nel XIX secolo.
I fondamenti dell'algebra booleana furono pubblicati da Boole nel 1854 con la pubblicazione
dell'opera "An investigation of the laws of thought"
Nel XX secolo la logica booleana fu adottata da Claude Elwood Shannon per spiegare il
funzionamento dei circuiti elettrici, poi elettronici e informatici.
Il sistema numerico binario
L'algebra booleana usa il sistema numerico binario.
E' un sistema numerico composto soltanto da due simboli: zero e uno.
B := { 0, 1 }
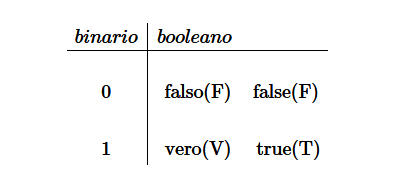
Nella logica booleana i due simboli assumono il significato di vero (V) e falso (F).
In informatica è usata la notazione inglese true (T) e false (F).
Pertanto, secondo me è preferibile abituarsi fin dall'inizio con le abbreviazioni inglesi.
La variabile che può assumere solo i valori vero (1) o falso (0) è detta variabile booleana.
Le operazioni tra le variabili booleane sono dette operazioni booleane.
Le operazioni booleane
Le principali operazioni binarie della logica booleana sono la somma, il prodotto e il
complemento.
Addizione logica
La somma logica di due valori booleani è 1 se almeno uno dei due fattori è uguale a 1
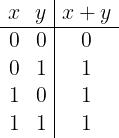
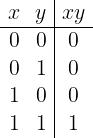
Moltiplicazione logica
Il prodotto logico di due valori booleani è 1 soltanto se entrambi gli addendi sono uguali a 1.
Complemento logico
Il complemento logico è l'operazione di negazione del valore booleano.
E' indicato con un trattino sopra la variabile.

Le funzioni booleane
Si dicono funzioni booleane le funzioni con variabili booleane sia nel dominio e sia nel
codominio (immagine).
Le funzioni booleane possono avere una (n=1) o più variabili booleane (n>1) nel dominio.
A sua volta anche il valore della funzione booleana è una variabile booleana.
Esempio
In questa funzione booleana sommo due variabili booleane (x+y) e lo moltiplico per x
La tavola di verità della funzione booleana è la seguente:
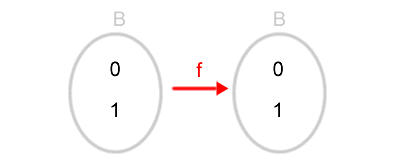
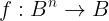
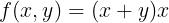

Come si può vedere anche il valore della funzione è un valore booleano.
Le leggi dell'algebra di Boole
Le operazioni tra le variabili booleane rispondono alle seguenti leggi dell'algebra booleana.



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





