ESP32 SMD Oven

IZ5FCY

Chi si marita fa bene, e chi no, fa meglio.

Il PID - Controllore proporzionale-integrale-derivativo

Un controllore proporzionale-integrale-derivativo (regolatore PID o regolatore a tre termini) è un meccanismo di loop di controllo che impiega il feedback (o retroazione) ampiamente utilizzato nei sistemi di controllo industriali e in una varietà di altre applicazioni che richiedono un controllo modulato continuamente. Un regolatore PID calcola continuamente un valore di errore e(t) come la differenza tra un setpoint desiderato (SP) e una variabile di processo misurata (PV) e applica una correzione basata su termini proporzionali, integrali e derivati (indicati con P, I e D), da cui il nome. I sistemi PID applicano automaticamente una correzione accurata e reattiva a una funzione di controllo. Un esempio quotidiano è il cruise control su un'auto, dove la salita di una collina ridurrebbe la velocità se si applicasse una potenza costante del motore. L'algoritmo PID del controller ripristina la velocità misurata alla velocità desiderata con un ritardo e una sovraelongazione minimi aumentando la potenza del motore in modo controllato. La prima analisi teorica e applicazione pratica del PID fu nel campo dei sistemi di governo automatico per le navi, sviluppati dai primi anni '1920 in poi. È stato poi utilizzato per il controllo automatico dei processi nell'industria manifatturiera, dove è stato ampiamente implementato nei controllori pneumatici e poi elettronici. Oggi il concetto PID è utilizzato universalmente in applicazioni che richiedono un controllo automatico accurato e ottimizzato. Operazione fondamentale La caratteristica distintiva del regolatore PID è la capacità di utilizzare i tre termini di controllo della influenza proporzionale, integrale e derivativa sull'uscita del regolatore per applicare un control- -lo accurato e ottimale. Il diagramma a blocchi a destra mostra i principi di come questi termini vengono generati e applicati. Mostra un regola- -tore PID, che calcola continuamente un valore di errore e(t) come la differenza tra un setpoint desiderato SP=r(t) e una variabile di processo misurata PV=y(t) : e(t)=r(t)-y(t) e applica una correzione basata su termini proporzionali, integrali e derivati. Il controllore tenta di ridurre al minimo l'errore nel tempo regolando una grandezza di controllo u(t), ad esempio l'apertura di una valvola di regolazione, a un nuovo valore determinato da una somma ponderata dei termini di regolazione In questo modello: • Il termine P è proporzionale al valore corrente dell'errore SP − PV e(t). Esempio, se l'errore è grande, l'uscita di controllo sarà proporzionalmente grande utilizzando il fattore di guadagno "Kp". L'utilizzo del solo controllo proporzionale comporterà un errore tra setpoint e il valore di processo perché il controllore richiede un errore per generare la risposta proporzionale della uscita. In condizioni di processo stazionarie si raggiunge un equilibrio, con un "offset" SP-PV stazionario. • Il termine I tiene conto dei valori passati dell'errore SP − PV e li integra nel tempo per dare il termine I. Ad esempio, se c'è un errore SP − PV residuo dopo l'applicazione del controllo proporzionale, il termine integrale cerca di eliminare l'errore residuo aggiungendo un effetto di controllo dovuto al valore cumulativo storico dell'errore. Quando l'errore viene eliminato, il termine integrale cesserà di crescere. Ciò comporterà che l'effetto proporzionale diminuisce al diminuire dell'errore, ma questo è compensato dall'effetto integrale crescente. • Il termine D è una migliore stima dell'andamento futuro dell'errore SP − PV, basato sull’attuale tasso di variazione. A volte viene chiamato "controllo anticipatorio", in quanto cerca di ridurre l'effetto dell'errore SP − PV esercitando un'influenza di controllo generata dalla variazione del tasso di errore. Più rapido è il cambiamento, maggiore è l'effetto di controllo o smorzamento.

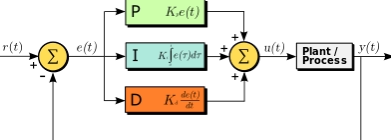
Diagramma a blocchi di un regolatore PID in un anello di retroazione. r(t) è la variabile di processo (PV) o il setpoint (SP) desiderato e y(t) è il PV misurato.